About Riemann Sum Formula
In the Riemann sum formula, we evaluate the approximation of the region's area under the curve on the graph, commonly called an integral. Riemann's sum introduces the precise definition of integral as the limit of a series which is infinite. Approximating the region's area of given lines or functions on the graph is a commonly used application of the Riemann sum formula. Riemann's sum formula is also evaluated for curves. The idea of calculating a sum is obtained by summing up areas of multiple simplified slices of the region, general shapes which are evaluated as multiple simplified slices of the region are rectangles, squares, parabolas, cubics, etc. Now gather the Riemann sum formula. Check out the list of Maths formulas prepared by the experts of Home tution.com
What is Riemann Sum Formula?
- Few methods which are used for finding an area in Riemann sum formula:
- Right and Left methods which are used to find area using endpoints of left and right of subintervals, respectively.
- Maximum and minimum methods: By this method, values of the largest and smallest endpoint of each sub-interval can be evaluated.
- Riemann Sum formula is:
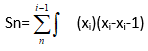
- Here,
- [a,b] = Closed interval classified into ‘n’ subintervals
- f(x) = continuous function on the given interval
- xi = Point belonging to the given interval [a,b]
- f(xi) = Value of function at x = xi
Riemann Sum formula