About Arc Length
The distance along a portion of the circumference of any circle or curve is best characterized as arc length (arc). The arc length is any distance along the curved line that makes up the arc. Arc refers to a portion of a curve or the circumference of a circle. Their shapes all have a curvature to them. An arc's length is greater than any straight line distance between its ends (a chord).
What is Arc Length?
The interspace between two locations along a portion of a curve is defined as the arc length. Any section of a circle's circumference is considered an arc. An arc's angle at any location is the angle generated by the two line segments that connect that point to the arc's end points. OP, for example, is the arc of the circle with centre Q in the diagram below. L denotes the arc length of this arc OP.

Arc Length Formula
Different formulas can be used to compute the length of an arc based on the unit of the arc's central angle. The centre angle can be measured in degrees or radians, and the arc length of a circle is calculated appropriately. The arc length formula for a circle is times the radius of a circle.
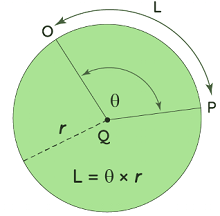
Arc length formula in radians expressed as, arc length = θ × r, θ is in radian.
Arc Length = θ × (π/180) × r, θ is in degree, where,
- L = Length of Arc
- θ = Central angle of the Arc
- r = Radius of circle
Arc Length Formula for Radians
Arc Length (L) = θ × r
where,
- L = Arc Length
- θ = Center angle of arc in radians
- r = Radius of circle
Arc Length of the Curve
- find arc length with radius and central angle
- find arc length without radius
- find arc length without central angle
Arc Length With Radius & Central Angle
- Length of Arc = θ × r, where θ is in radian.
- Length of Arc = θ × (π/180) × r, where θ is in degree.
Arc Length Without the Radius
Central angle and the sector area:
- Multiply the sector area by 2 & further, divide result by central angle in radians.
- Get square root of the result of the division.
- Multiply this obtained root by central angle again to get arc length.
- The units of thus calculated arc length will be square root of sector area units.
Central angle & chord length:
- Divide central angle in radians by 2 & further, perform the sine function on it.
- Divide given chord length by twice result of step 1. This calculation gives you radius as result.
- Multiply the radius by central angle to get the arc length.
Arc Length Without the Central Angle
Radius & the sector area:
- Multiply the sector area by 2.
- Then divide result by the radius squared (the units should be the same) to get the central angle in radians.
- Multiply central angle by the radius to get the arc length.
Radius and chord length:
- Divide the chord length by twice the given radius.
- Find the inverse sine of the obtained result.
- Double the result of the inverse sine to get the central angle in radians.
- Multiply the central angle by the radius to get the arc length.
Important Notes on Arc Length
- Arc Length = θ × r, θ is in radian.
- Arc Length = θ × (π/180) × r, θ is in degree.