About Simpson's Rule
One of the formulas used to find the approximate value of a definite integral is Simpson's rule. An integral possessing lower and upper boundaries is called a defined integral. To assess a definite integral, we usually first integrate (using integration techniques) and then apply the limits using the fundamental theorem of calculus. However, sometimes we are unable to calculate an integral using any integration approach, and we do not have a specific function to integrate; instead, we have some observed values (in the case of experiments). Simpson's rule aids in approximating the value of the definite integral in such instances.
What do you mean by Simpson's Rule?
By approximating the area under the graph of function f, Simpson's technique is used to find the value of a definite integral (that is, of the type ba f(x) dx) (x). We calculate the area under a curve (a definite integral) using the Riemann sum by dividing the area under the curve into rectangles, but we evaluate the area under a curve using Simpson's formula by dividing the whole area into parabolas. Simpson's 1/3 rule (pronounced Simpson's one-third rule) is another name for Simpson's rule.
The formula of Simpson's Rule:
To estimate an integral, we can use Riemann's left sum, Riemann's right sum, midpoint rule, trapezoidal rule, Simpson's 1/3 rule, and other numerical methods. Simpson's rule, however, provides the most precise estimate of a definite integral. The Simpson's rule formula is: f(x) = y, which is evenly spread between [a,b].
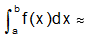(h/3)[f(x0) + 4f(x1) + 2f(x2) + .....+2f(xn-2) + 4f(xn-1) + f(xn)]
- where, n is an even number that represents the number of subintervals that should be divided into the interval [a, b].
- (n is usually mentioned in the problem)
- x0 = a, xn = b
- h = [ (b - a) / n]
- These x0, x1, ...., xn are ends of the n subintervals.
Error Bound of Simpson's Rule:
Simpson's rule only yields a rough estimate of the integral value, not an exact number. As a result, there is always an error, which may be determined using the method below.
Error bound in Simpson's rule = {M(b−a)5}/{180n4},
where |f(4)(x)|≤M
Check out the list of Maths formulas prepared by the experts of Home tution.com
Download free pdf of Total Simpson's Rule Its Use And Solved Examples
