About Tangent Formulas
Tangent formulas are the formulas about tangent function in trigonometry. The tangent function is the ratio of the opposite side to the adjacent side. There are many formulas related to tangent function which can be derived from various trigonometric formulas. Now take a look at tangent formulas along with a few solved examples.
What Are Tangent Formulas?
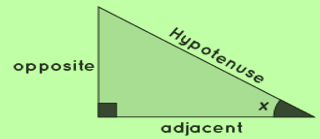
Tangent formulas tell about tan function. Take a right-angled triangle with one of its acute angles be x. Then tangent formula will be, tan x = (opposite side) / (adjacent side), here "opposite side" is the side opposite to angle x, and "adjacent side" is the side which is adjacent to angle x. There are so many other formulas in trigonometry that will define a tan function which you will see in the below image. Check out the List of Maths Formulas.
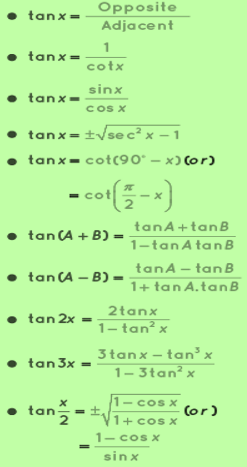
Tangent Formulas Using Reciprocal Identity
As we already know that tan function and cot function are reciprocals of each other. i.e., if tan x = a / b, then cot x = b / a. Thus, tangent formula using one reciprocal identities will be
tan x = 1 / (cot x)
Tan Formula Using Sin and Cos
As we already know that
sinx = (opposite)/(hypotenuse),cosx = (adjacent)/(hypotenuse),tanx = (opposite)/(adjacent)
(sinx)/(cosx) = [(opposite)/(hypotenuse)]/[(adjacent)/(hypotenuse)] = (opposite)/(adjacent) = tanx
Hence, the tangent formula in terms of sin and cos is,
tan x = (sin x) / (cos x)
Tangent Formulas Using Pythagorean Identity
One of the Pythagorean identities tells about the relation between sec and tan. It tells, sec^2x – tan^2x = 1, for any x. We can evaluate this for tan x. Now take a look at how.
Sec2x – tan2x = 1
On subtracting sec^2x from both sides,
-tan2x = 1 – sec2x
On multiplying both sides by -1,
Tan2x = sec2x - 1
Taking square root on both sides,
tan x = ± √( sec^2x - 1)
Download a free pdf of Tangent Formulas Its Use And Solved Examples
