Vertex Formula Definition
The coordinates of the point where the parabola crosses its axis of symmetry are found using the parabola's vertex formula. The point is the vertex (h,k). The usual equation for a parabola is y = ax2+bx+c, as we all know. The vertex point is the bottom of the U-shaped curve if the coefficient x2 is positive, while the vertex point is the top of the U-shaped curve if it is negative. The vertex where the parabola is either minimum (when it expands up) or maximum (when it opens down) and the parabola turns (or changes) direction. For more Maths formulas click on the main page.
The vertex formula aids in the determination of a parabola's vertex coordinates. A parabola's typical form is y = ax2 + bx + c. The parabola's vertex form is y = a(x - h)2 + k. There are two methods for determining vertex (h, k). They are:
- (h, k) = (-b/2a, -D/4a), D(discriminant) = b2 - 4ac
- (h,k), where h = -b / 2a & evaluate y at h to find k.
Vertex Formulas and its use???????
2 vertex formulas to find the vertex is:
Formula 1:(-b/2a, -D/4a) = (h, k)
where,
- D - denominator
- h,k - coordinates of the vertex
Formula 2:-b / 2a = x-coordinate of the vertex
Derivation of Vertex Formulas
Formula 1:
The typical form of a parabola is y = ax2 + bx + c, as we know. By completing the squares, we can transform them to the vertex form y = an (x - h)2 + k.
Subtract c from both sides:
y - c = ax2 + bx
Take "a" as the common factor:
y - c = a (x2 + b/a x)
half coefficient of x is b/2a & its square is b2/4a2. Adding & subtracting this on the right side (inside the parentheses):
y - c = a (x2 + b/a x + b2/4a2 - b2/4a2)
x2 + b/a x + b2/4a2 as (x + b/2a)2. Thus, the above equation becomes:
y - c = a ( (x + b/2a)2 - b2/4a2)
Distributing "a" on the right side & adding "c" on both sides:
y = a (x + b/2a)2 - b2/4a + c
y = a (x + b/2a)2 - (b2 - 4ac) / (4a)
Comparing this with y = a (x - h)2 + k, we get:
h = -b/2a
k = - (b2 - 4ac) / (4a)
b2 - 4ac = discriminant (D).
Thus, vertex formula is: (h, k) = (-b/2a, -D/4a) and D = b2 - 4ac
Formula 1:
If memorising the above method proves challenging, simply recall the formula for the x-coordinate of the vertex and insert it into the given equation y = ax2 + bx + c to obtain the y-coordinate of the vertex.
x-coordinate of the vertex(h) = -b / 2a
Alternatively, if you don't want to use any of the previous formulas, you can manually complete the square to transform y = ax2 + bx + c to the form y = an (x - h)2 + k and identify the vertex (h, k).
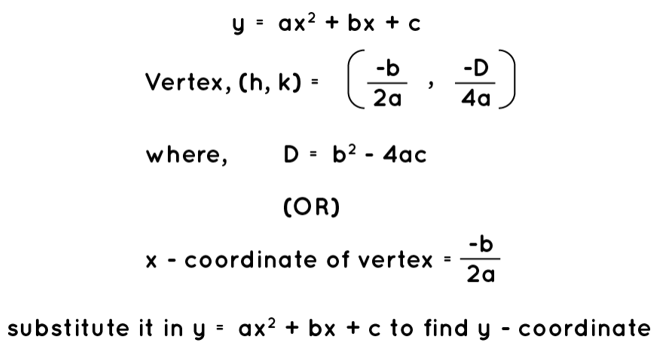
Solved Example for Vertex Formula
Example-1
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, – 2). The third vertex lies on
y = x + 3. Find the third vertex.
Sol.Let the third vertex be (x3, y3), area of triangle = 1/2|[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]|
As x1= 2, y1 = 1, x2 = 3, y2 = 2, Area of triangle = 5
5 =1/2|2(–2 –y1) + 3(y1 – 1) + x3(1 + 2)|
10 = |3x3 + y3 – 7|
3x3 + y3 =19
Taking negative sign
3x3 + y3 – 7 = – 10
3x3 + y3 = 17 ----(1)
Taking negative sign
3x3 + y3 – 7 = – 10
3x3 + y3 = –3 ----(2)
Given that (x3, –y3) lies on y = x + 3
So, – x3 + y3 = 3---(3)
Solving eq. (1) and (3), x3 =7/2, y3 = 13/2
Solving eq. (2) and (3), x3 =-3/2, y3 = 3/2
So the third vertex are 7/2 and 13/2
