About Exterior Angle Theorem
According to the external angle theorem, when the triangle's side is extended, the resulting exterior angle is equal to the sum of the measurements of the triangle's two opposed internal angles. The theorem can be used to calculate the length of an unknown triangle angle. To use the theorem, we must first determine the triangle's exterior angle and then the two adjacent remote interior angles. You can get all Maths formulas on one-page visit the Maths Formulas section of HT.
What is Exterior Angle Theorem?
The measure of an exterior angle is equal to the sum of the measures of the two opposite(remote) interior angles of the triangle, according to the external angle theorem. Let's review some basic triangle angle properties: Internal angles of a triangle always add up to 180 degrees. There are six outside angles, and this theorem is applied to each of them. Because they constitute a linear pair of angles, an exterior angle is supplementary to its adjacent interior angle. The angles generated between the side of the polygon and the extended adjacent side of the polygon are known as exterior angles.
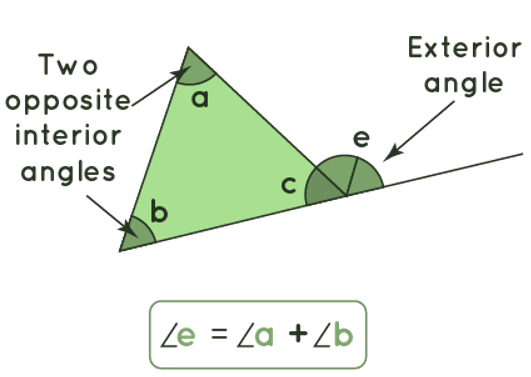
- With the properties of a triangle, we may prove the exterior angle theorem. Take a look at an Δ ABC.
- The 3 angles a + b + c = 180 (angle sum property of a triangle) ----- Eq 1
- c = 180 - (a+b) ----- Eq 2 (rewriting equation 1)
- e = 180 - c ----- Eq 3 (linear pair of an angles)
- Substituting value of c in eq 3, we get
- e = 180 - [180 - (a + b)]
- e = 180 - 180 + (a + b)
- e = a + b
- Hence proved.
Exterior Angle Theorem Proof
Consider a ΔABC. a, b & c are angles formed. Extend side BC to D. Now an exterior angle ∠ACD formed. Draw a line CE parallel to AB. Now x & y are the angles formed,
∠ACD = ∠x + ∠y
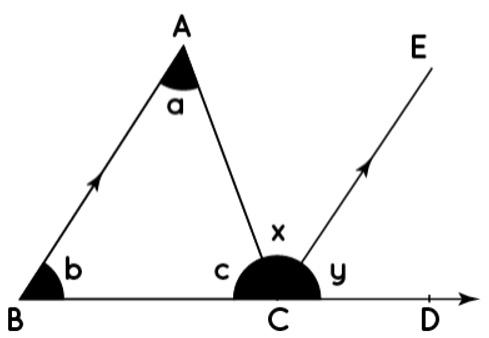
| Statement | Reason |
| ∠a = ∠x | Pair of alternate angles. (Since BA is parallel to CE and AC is the transversal). |
| ∠b = ∠y | Pair of corresponding angles. (Since BA is parallel to CE and BD is the transversal). |
| ∠a + ∠b = ∠x + ∠y | From the above statements |
| ∠ACD = ∠x + ∠y | From the construction of CE |
| ∠a + ∠b = ∠ACD | From the above statements |
As a result, the total of the two opposed internal angles equals the triangle's outer angle.
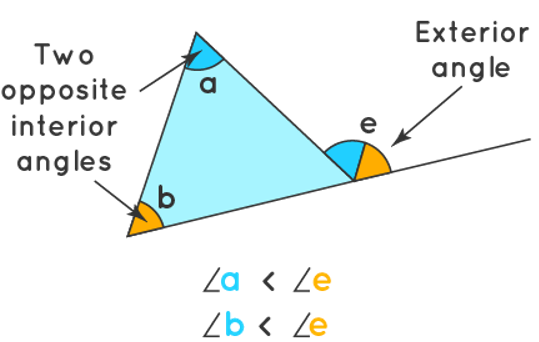
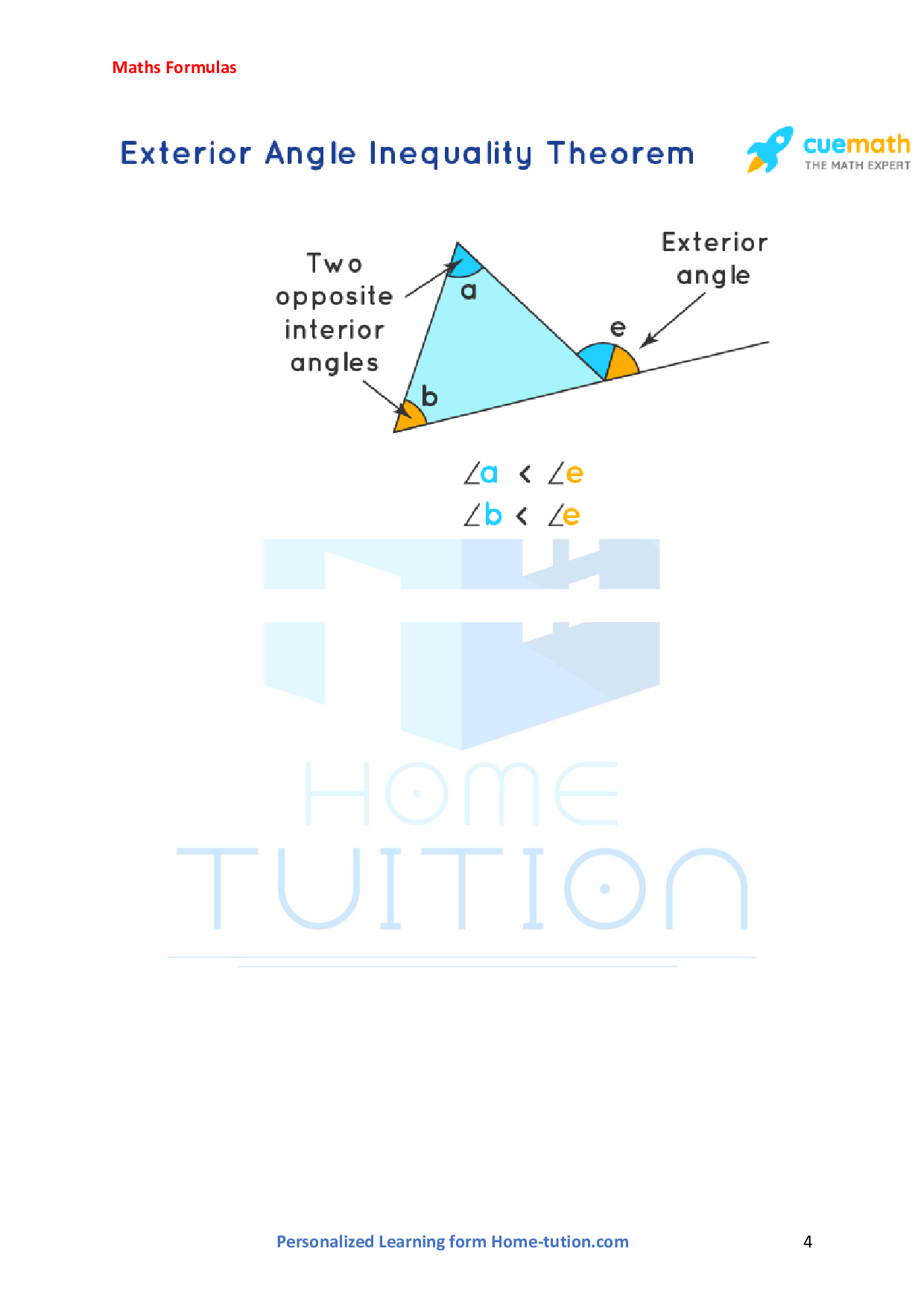
Exterior Angle Inequality Theorem
The measure of any outside angle of a triangle is bigger than either of the opposite interior angles, according to the exterior angle inequality theorem. All of a triangle's six external angles satisfy this requirement.
Important notes about Exterior Angle Theorem
The measure of an exterior angle is equal to the sum of the measures of the two distant interior angles of a triangle, according to the external angle theorem.
The measure of any outside angle of a triangle is bigger than either of the opposite interior angles, according to the exterior angle inequality theorem.
The adjacent inner angle and the external angle are complementary. The total of a triangle's outer angles is 360 degree.
Exterior Angle Inequality Theorem
Download pdf of Exterior Angle Theorem Formula
