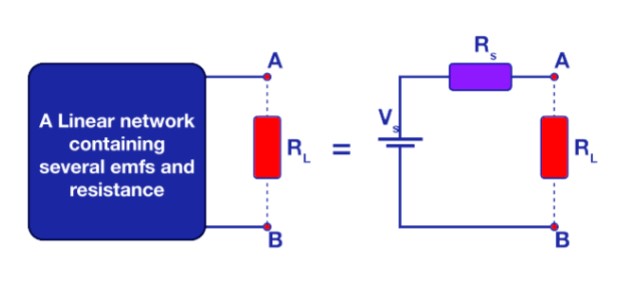
Thevenin's Theorem

Thevenin’s Theorem Explanation

Thevenin's theorem is a powerful concept in electrical engineering that simplifies the analysis of complex linear circuits. It states that any complex network of resistors, voltage sources, and current sources can be reduced to a single equivalent circuit. This equivalent circuit consists of a single voltage source V_s and a series resistor R_s.

In the Thevenin equivalent circuit, the original circuit's resistive elements are consolidated into a single equivalent resistance R_s. Similarly, multiple independent voltage sources are replaced by a single equivalent voltage source V_s.

Thevenin’s Theorem Example

Thevenin’s Theorem can be understood with the help of the following example

Example:

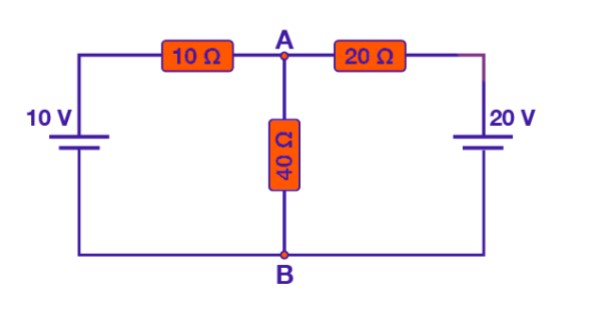
• Step 1: Begin by removing the load resistor R_load, such as 40 ohms in this example, to simplify the circuit.
• Step 2: To eliminate the effect of internal resistance in voltage sources within a circuit, short-circuiting all voltage sources is essential (setting v=0). If there are any current sources present, they should be open-circuited to similarly remove their internal resistance. This procedure is crucial for establishing ideal voltage or current sources, optimizing the circuit for accurate analysis and solution.
• Step 3: To find the equivalent resistance of a circuit, you start by removing the load resistance and identifying the voltage sources.

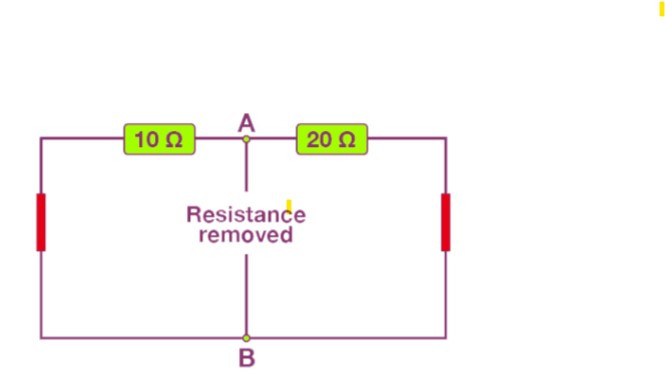
• In a given example, resistors like 10 Ω and 20 Ω are connected in parallel with a 20 Ω resistor.

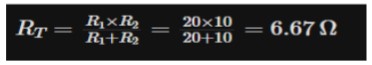
• By applying the parallel resistor formula, the equivalent resistance of the circuit is calculated to be 6.67 ohms."
• Step 4: Find the equivalent voltage.

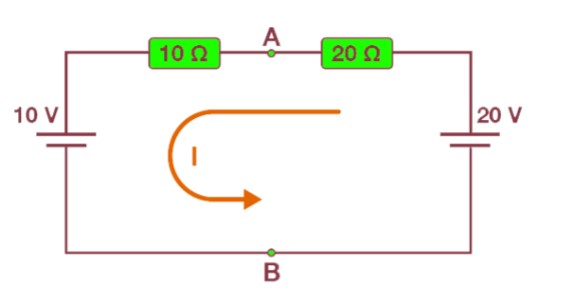
• To find the equivalent voltage, reconnect the voltage sources within the circuit. Calculate the current circulating through the loop using the equation: "as the voltage between Vs = VAB."

Since both resistors carry identical currents, we can calculate the voltage drop across them using either of these formulas:

• For the 20-ohm resistor: \( V_{AB} = 20V - (20 \Omega \times 0.33A) = 13.33V \)
• For the 10-ohm resistor: \( V_{AB} = 10V + (10 \Omega \times 0.33A) = 13.33V \)

This means both resistors experience the same voltage drop across them.

• Step 5: Construct the Thevenin equivalent circuit, which comprises a single voltage source V_s (e.g., 13.33 V) and a series resistor R_s (e.g., 6.67 ohms).

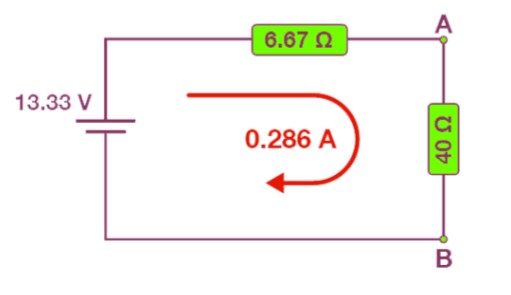
We can calculate the current in the circuit as:

Application of Thevenin’s Theorem

Thevenin’s theorem is widely applicable in both AC and DC circuits, particularly those containing linear components such as resistors, inductors, and capacitors. By replacing a complex circuit with a simpler equivalent, it facilitates easier analysis and design, making it a fundamental tool in electrical engineering.