De Morgan’s First Law

De Morgan's Law is a set of rules in boolean algebra that use complements to connect the intersection and union of sets.

According to De Morgan's Law, two conditions must be met. These conditions are typically used to simplify complex expressions.This makes it easier to calculate and solve complex boolean expressions.

De Morgan's Law states that the complement of the union of two sets is equal to the intersection of their separate complements. Additionally, the complement of the intersection of two sets is equal to the union of their individual complements.

These laws can be easily visualized using Venn diagrams. In this article, we will look at De Morgan's Law.

De Morgan's Law Introduction 

According to De Morgan's First Law, the complement of the union of two sets is the intersection of their complements. De Morgan's second law states that the complement of the intersection of two sets is the union of their complements. These two laws are collectively known as De Morgan's Law.De Morgan's first law can be written as (A ∪ B)' = A' ∩ B'. These complement laws in set theory relate the intersection and union of sets.

State De Morgan’s Law

De Morgan's Law describes the relationship between three fundamental set operations: set complement, set union, and set intersection.

According to De Morgan's Law, the complement of the union of two sets is the intersection of their complements, and the complement of the intersection of two sets is the intersection of their complements.

De Morgan’s First law

It states that the complement of any two sets union is equal to the intersection of their complements. De Morgan's theorem describes the relationship between the union of two sets and their intersection of sets using the set complement operation.

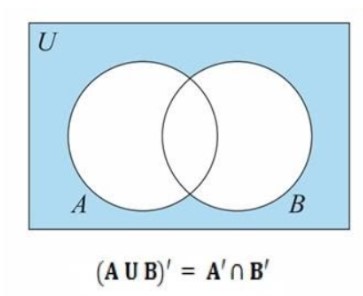
Consider any two sets A and B , the mathematical relation of De Morgan’s Law is given by, 

(AUB)' = A'B'

Proof Of De Morgan’s First Law

There are two proofs provided for De Morgan's Law, one mathematical and one using a Venn diagram.

De Morgan’s first law tells that, (AUB)' = A'B'

Mathematical Approach

Let us consider P=(AUB)' and Q= A'B'

Let x be any element of P, then xP(AUB)'

x(AUB)

xA or xB

xA' and xB'

xA'B'

xQ

Therefore, PQ……..(i)

Again, let y be an arbitrary element of Q then yQA'B'

yA' and yB'

yA or yB

y(AUB)

y(AUB)'

yP

Therefore, QP……(ii)

Now combine (i) and (ii) we get, P=Q

i.e. (AUB)' = A'B'

Venn Diagram Method

Consider two sets, A and B, and consider how the union of sets is represented by shading the entire portion of two sets.

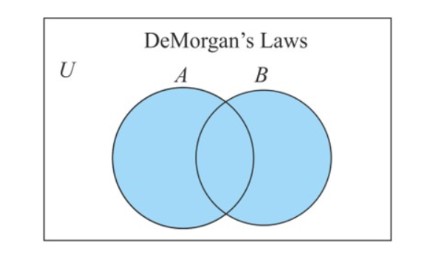
Except for A and B, the AB' Venn's diagram depicts the entire Union region.

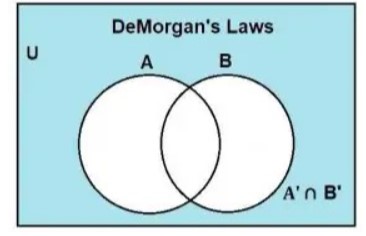
We already know that the complement of two sets, A and B, is represented by shading all regions of union except the given set.

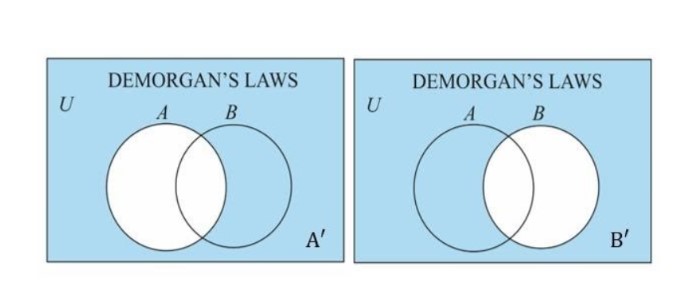
The intersection of the complements of two sets is depicted in the Venn diagram below.

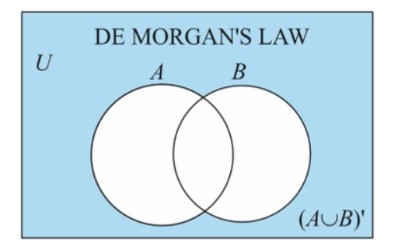
Thus, by using the venn diagrams, we can say that (AUB)' = A'B'

Application Of De Morgan’s Law

De Morgan's law can be found in both basic and advanced algebra. Because it helps to reduce difficult statements, this law is commonly used in most engineering sectors to develop hardware and simplify operations. Some examples of De Morgan's law are given below:

• Demorgan's law is commonly used in computer programming. This law contributes to fewer lines of logical statements expressed in codes. As a result, it contributes to overall code optimization. Furthermore, these laws make SAS code verification much easier and quicker.
• In Digital Electronics, De Morgan's Law: It is possible to see the application of De Morgan's law in electronic engineering for the development of logic gates. This mathematical equation requires only the NAND (AND negated) or NOR (OR negated) gates. As a result, the hardware costs less. In practice, NAND, NOT, and NOR gates are also simple to implement.

Conclusion

Demorgan's law, which describes the relationship between the complement of union and the intersection of two sets, has been studied in this article. The union, intersection, and complement of sets were discussed in this article. This article also provided a mathematical proof for De Morgan's laws. It also discussed the visual proof of De Morgan's law using Venn diagrams.

Also Read - 

• Factors of 28
• Factors of 32
• Differential Calculus and Approximation
• Difference between Area and Volume
• Cubes from 1 to 50
• Cubes from 1 to 50
• Curved Line