Decimal Expansion Of Rational Numbers

A rational number is a number that can be expressed as a fraction, where the numerator and denominator are both integers, and the denominator is not zero. In other words, a rational number is a number in the form of p/q, where p and q are integers and q is not equal to 0.

Rational numbers can also be expressed as decimal numbers. The decimal form of a rational number can be either terminating or non-terminating.

A rational number's non-terminating decimal form can be either recurring or non-recurring. To convert a rational number to its decimal form, we need to follow certain rules.

In this article, we will learn about the decimal expansion of rational numbers.

Decimal Expansion Of Rational Numbers Introduction

Let's first define what a rational number is before looking at how to represent the decimal expansion of rational numbers. A rational number is any number that can be expressed as the fraction p/q, where p and q are integers and q is not equal to 0. When these numbers are simplified further, they produce decimals.

Examples of rational numbers include 6, 8, -1, and 45.

Definition of Decimal Expansion of Rational Numbers

Rational numbers are numbers in the form p/q, where p and q are integers, and q is not equal to 0. Some examples of rational numbers include:

• 3/2, -4/15, 219/219 (which can be simplified to 1)
• 0, since we can write 0 as 0/1, which is the quotient of two integers with a non-zero denominator
• Every natural number, such as 1 = 1/1, 2 = 2/1, and so on. In general, if n is a natural number, then we can write n = n/1, which is a rational number.
• Every integer, since we can write any integer m as m/1, which is a rational number.

How to Expand Rational Numbers in Decimals?

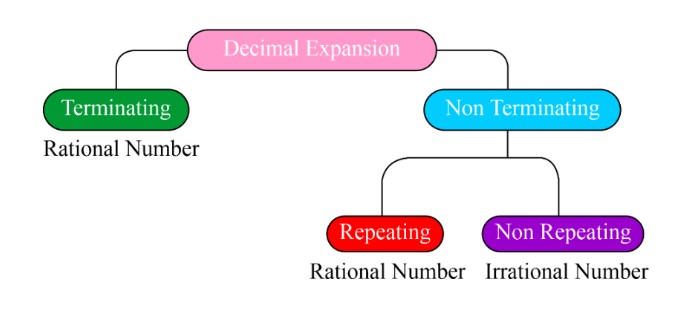
The decimal expansion of a rational number is obtained by dividing its numerator by its denominator. The decimal numbers thus obtained can be classified into two types.

1. Terminating decimals
2. Non-terminating decimals

1. Terminating decimals

The terminating decimal numbers are decimal numbers with a finite number of digits after the decimal point. Their decimal places are limited. These decimal numbers are referred to as exact decimal numbers.

We can represent these decimal numbers pq, where p and q are integers and q0.

For example, 2.3,4.43 are the terminating decimal numbers.

2.3 is represented as 2310, when p=23 and q=10 and the number of decimal places =1.

4.433 is represented as 44331000, when p=4433 and q=1000 and the number of decimal places =3.

2. Non - Terminating Decimal Numbers

Non-terminating decimal numbers are those that have an infinite number of digits after the decimal point.

For example, 0.3333.......,4.4333....,5.346710... are examples of non - terminating decimal numbers.

Non-terminating decimal numbers are classified into two types: recurring decimals and non-recurring decimals.

a. Recurring Decimals

Recurring decimal numbers have an infinite number of digits after the decimal point, and the digits are repeated at equal intervals after the decimal point.

For example, 0.111...,4.444.....,5.2323.....etc., are the recurring decimals.

The numbers that can be represented in pq form where q0 are known as rational numbers.

b. Non - Recurring Decimals

Non-recurring decimal numbers have an infinite number of digits after the decimal point and the digits are not repeated at equal intervals after the decimal point.

For example, 0.1224589.....,5.34268.... etc., are non-recurring decimals.

We can not represent non - recurring decimals in pq form.

The numbers that can not be represented in pq form where q0 are known as irrational numbers. Thus, we can say that non - terminating decimals are irrational numbers. 

Methods to Expand Rational Numbers in Decimals

The recurring decimals that are expressed as rational numbers can be terminating or non-terminating. Let us look at some rational numbers and determine their decimal expansion.

• Example 1 : Find the decimal expansion of 13.

Divide the numerator by denominator

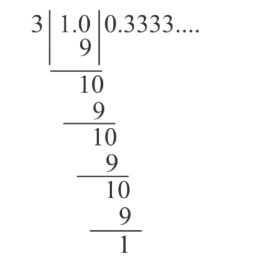
The decimal expansion of 13 is 0.3333....

• Example 2 : Find the decimal expansion of 17.

Divide the numerator by denominator

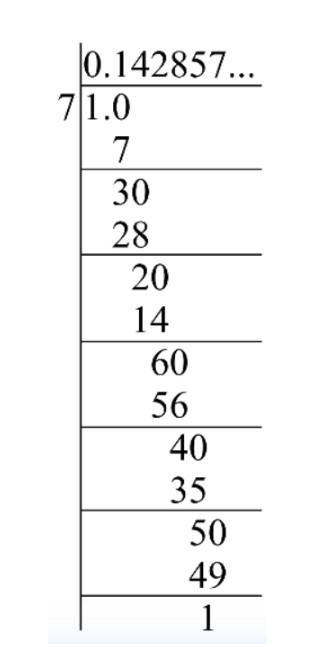
The decimal expansion of 17 is 0.142857....

• Example 3 : Find the decimal expansion of 78.

Divide the numerator by denominator

The decimal expansion of 78 is 0.875.

Now , we can see three things

(i) After a certain stage, the remainder either becomes 0 or begins to repeat itself.

(ii) The repeating string of remainders has fewer entries than the divisor.

In 13, only one number, i.e, 1 repeats itself as a reminder. In 17, there are six entries 3,2,6,4,5,1 in the repeating string of remainders, and 7 is a divisor.

(iii) If the remainder repeats , then we get a repeating block of digits in the quotient. For 13,3 repeats in the quotient and for 17, we get the repeating block as 142857.

Terminating Decimal Expansion Of Rational Numbers

The terminating decimal expansion indicates that the decimal number ends after a specific number of digits after the decimal point. In the example of 78, we found that the remainder becomes zero after some steps, and we got the decimal expansion of 78 is 0.875 using the long division method. There is an alternative method to long division for determining the terminating decimal numbers.

A rational number is terminated if it can be represented as p2n5m.

The rational number whose denominator has no prime factors other than 2 and 5 gives a terminating decimal number.

Consider the example 78.

Now, the denominator is 8 that means 23. To make the denominator 10's power, we need to multiply the denominator and the numerator by 53.

7532353=8751000=0.875

Conclusion

We learned about rational numbers, rational decimal expansions, and how to convert rational numbers to decimal form in this article. We discovered that the long division method can be used to find the decimal form of any rational number. Every non-terminating decimal cannot be expressed as a rational number, as we have seen.

Also Read - 

• Factors of 28
• Factors of 32
• Differential Calculus and Approximation
• Difference between Area and Volume
• Cubes from 1 to 50
• Cubes from 1 to 50
• Curved Line