Percentages
The term "percentage" originates from the Latin phrase "per centum," which translates to "by the hundred." Percentages represent fractions where the numerator is always 100.
What is Percentage?
A percentage represents a fraction or ratio where the whole is always 100. For instance, if Sam got 30 percent on his math test, he scored 30 points out of 100. In fraction form, this is 30/100, and in ratio form, it's 30:100.
It's a fraction with 100 as the bottom number, and the symbol "%" stands for "percent."
Calculation of Percentage
Technique 1: Using the Percentage Formula
The basic formula for calculating a percentage is:Percentage = (Part / Whole) x 100To use this formula:
- Identify the "part" and the "whole" values in the problem.
- Divide the part by the whole.
- Multiply the result by 100 to get the percentage.
Example:
If a store sold 25 items out of a total of 50 items, the percentage of items sold would be:
Percentage = (25 / 50) x 100 = 50%
Technique 2: Using Proportions
Another way to calculate percentages is by setting up a proportion:Part / Whole = x / 100To use this technique:
- Set up the proportion with the part, whole, and 100 (representing 100%).
- Cross-multiply to solve for the unknown percentage (x).
- Simplify the result to get the final percentage.
Also Check: Prime Numbers from 1 to 100
Example:
If a student scored 80 points out of a total of 100 points on a test, the percentage would be:
80 / 100 = x / 100
Solving for x: 80 = x
Therefore, the percentage is 80%Both techniques provide the same result, but the proportion method may be more intuitive for some problems. The key is to correctly identify the "part" and "whole" values in the given scenario.
How to get a Percentage?
Percentage is a way to express parts out of a whole, where each part represents one-hundredth of the whole. For instance, 1 percent equals 0.01 or 1/100.
To find the percentage of two or more numbers that add up to 100, divide each individual number by the total and multiply by 100.
For example, Rohit bought tiles in three different colors for his home. The table below shows how many tiles of each color he purchased.
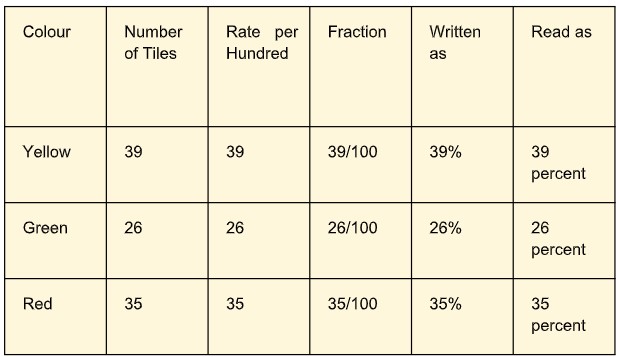
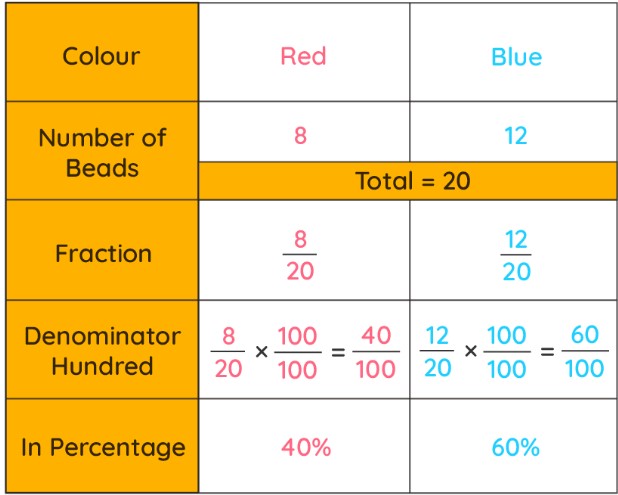
If the total isn't 100, we convert fractions into equivalent fractions with a denominator of 100.
For instance, Mohit's bracelet has 20 beads in total, with some beads red and others blue. The table below illustrates the percentage of red and blue beads among these 20 beads.
Formula to Calculate Percentage
Percentage= (Value/Total Value)×100
Also Check: Even Numbers
Percentage Difference Between Two Numbers
"The percentage difference measures how much a quantity changes over time, shown as a percentage. It reflects the growth or decline of something in terms of percentages. For example, it could indicate an increase in population or a decrease in poverty. When calculating percentage differences, two scenarios may arise:
- Calculate the percentage increase.
- Determine the percentage decrease."
Also Check: Co-Prime Numbers
How to Calculate Percentage Increase?
Percentage Increase= (Increased Value-Original value)/Original value × 100
How to Calculate Percentage Decrease?
Percentage Decrease= (Original value-Decreased Value)/Original Value × 100