Factor Theorem

In mathematics, the factor theorem helps in fully factoring a polynomial. This theorem links the polynomial's factors to its zeros.

Introduction to Factor Theorem

The Factor Theorem states that for a polynomial f(x) of degree n ≥ 1 and any real number a, (x - a) is a factor of f(x) if and only if f(a) = 0. This means that if (x - a) is a factor of f(x), then substituting a into the polynomial results in zero, confirming the theorem.

Let's explore this theorem with some examples to understand its application.

What is the Factor Theorem?

The Factor Theorem is a method used to determine the factors and roots of polynomials. It states that a polynomial f(x) has a factor (x - a) if and only if f(a) = 0. This is a key concept in polynomial factorization.

Proof

We will now prove the Factor Theorem, which allows us to factorize polynomials. Suppose a polynomial f(x) is divisible by (x - c), then f(c) = 0. According to the Remainder Theorem:

f(x) = (x - c)q(x) + f(c)

Here, f(x) is the polynomial, and q(x) is the quotient polynomial. Since f(c) = 0:

f(x) = (x - c)q(x) + 0
f(x) = (x - c)q(x)

Thus, (x - c) is a factor of the polynomial f(x).

Another Method

Using the Remainder Theorem again:

f(x) = (x - c)q(x) + f(c)

If (x - c) is a factor of f(x), then the remainder must be zero, meaning (x - c) exactly divides f(x). Therefore, f(c) = 0.

The following statements are equivalent for any polynomial f(x):

• When f(x) is divided by (x - c), the remainder is zero.
• (x - c) is a factor of f(x).
• c is a root or solution of f(x).
• c is a zero of the function f(x) or f(c) = 0.

How to Use Factor Theorem

To find the factors of a polynomial using the factor theorem, follow these steps:

1. If f(-c) = 0, then (x + c) is a factor of f(x).
2. If pdc = 0, then (cx - d) is a factor of f(x).
3. If p - dc = 0, then (cx + d) is a factor of f(x).
4. If p(c) = 0 and p(d) = 0, then (x - c) and (x - d) are factors of p(x).

Instead of using polynomial long division, the factor theorem and synthetic division are often easier ways to find factors. The factor theorem helps identify known zeros of a polynomial, reducing its degree and making it simpler to solve.

When dividing a polynomial by a binomial factor, if the remainder is zero, the binomial is indeed a factor of the polynomial. This is known as the factorization theorem.

Other Methods to Find Factors

Besides the factor theorem, you can use:

• Polynomial Long Division
• Synthetic Division

Polynomial Long Division Example

For f(x) = x² + 2x - 15:

Solve x² + 2x - 15 = 0:

x² + 5x - 3x - 15 = 0
x(x + 5) - 3(x + 5) = 0
(x - 3)(x + 5) = 0

Thus, x = -5 or x = 3 are the roots.

Synthetic Division Example

Using f(x) = x² + 2x - 15 and dividing by x - 3:

Place 3 on the left and use the coefficients 1, 2, and -15 from f(x).

Perform synthetic division to verify that the remainder is zero, confirming that x - 3 is a factor.

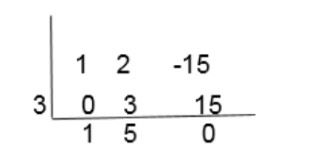
Because the remainder is zero, 3 is a solution of the polynomial. Solving equations of degree 3 or higher is more complex, so we often use simpler linear and quadratic equations instead.