A disjoint set, also called a partition, is a math concept that describes a group of sets that don't share any elements. In simpler terms, the sets in this group do not overlap with each other. The study of disjoint sets is a key part of set theory and is widely used in fields like graph theory and computer science.
Introduction to Disjoint Set
Disjoint sets, also known as partition sets, are a key concept in both mathematics and computer science. In math, they describe sets that have no elements in common. In computer science, they are used for operations like union and intersection of sets. This article will explore disjoint sets, including their definition, examples, and visual representation. We will also solve some examples and answer frequently asked questions about disjoint sets.
Also Check: Discrete Mathematics
What are Disjoint Sets?
Disjoint sets are sets that do not share any elements. They are completely separate and do not overlap. For instance, consider two sets: A = {1, 2, 3} and B = {4, 5, 6}. These sets are disjoint because they have no elements in common.
Definition of Disjoint Set
Mathematically, a disjoint set is a collection of sets {S1, S2, ..., Sn} where the intersection of any two sets in the collection is the empty set. This is represented as:
Si ∩ Sj = ∅ for all i ≠ j
This means that no element can belong to more than one set in the collection. The sets are pairwise disjoint.
Also Check: Continuity and Discontinuity
Venn Diagram for Disjoint Sets
A Venn diagram can be used to visualize disjoint sets. In a Venn diagram, sets are shown as circles that do not overlap, indicating that they have no elements in common.
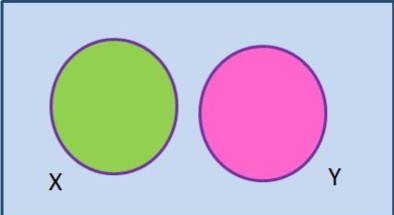
When Are Two Sets Disjoint?
Two sets are disjoint when they do not share any elements. For example, sets A = {1, 2, 3} and B = {4, 5, 6} are disjoint because A ∩ B = ∅.
Let's consider an example with sets X = {1, 3}, Y = {2, 3}, and Z = {2, 5}. We need to check each pair to see if they are disjoint:
X ∩ Y = {1, 3} ∩ {2, 3} = {3} Y ∩ Z = {2, 3} ∩ {2, 5} = {2} X ∩ Z = {1, 3} ∩ {2, 5} = ∅
From this, we see that X and Z are disjoint sets.
Also Check: Difference Between Variance and Standard Deviation
Pairwise Disjoint Sets
Pairwise disjoint sets are sets that don't share any elements. In other words, if you look at any two sets and check their common elements, you'll find none. This concept is useful in various areas of mathematics because it lets us consider sets as entirely separate groups.
For instance, in graph theory, we use pairwise disjoint sets to show connected components in a graph. Each set stands for a connected part, and the sets are pairwise disjoint because no single vertex can be in more than one connected component.
Union of Disjoint Sets
The union of two disjoint sets is a set that contains all the elements from both sets. In mathematical terms, the union of sets A and B is written as A ∪ B. This means it includes every element from set A, every element from set B, or elements from both.
The union operation is a key idea in set theory, used to merge sets into a larger one. When dealing with disjoint sets, the union combines two sets that have no elements in common, resulting in a new set that remains disjoint.
For instance, let’s take two disjoint sets: A = {1, 2, 3} and B = {4, 5, 6}. The union of these sets is A ∪ B = {1, 2, 3, 4, 5, 6}. This new set is still disjoint because no element is shared between A and B.