Difference Between Permutation and Combination

Permutation and combination are two ideas used in math for counting and probability.

Permutation is about arranging things in a certain order. The order matters here. You can find the number of permutations by using this formula: n!/(n-r)!, where n is the total number of items, and r is the number of items you are arranging.

Combination is about choosing things where the order doesn't matter. To find the number of combinations, you use this formula: n!/(r!(n-r)!), where n is the total number of items, and r is the number of items you are choosing.

In simple words, permutation is like lining up items in a specific way, while combination is like picking items from a group without worrying about the order.

Also Check: Diffrence Between area and Volume | Diffrence Between Cube and Cuboid | Diffrence Between Mean, Median Mode

Definition of Permutation

A permutation is when you arrange a group of items in a specific order. It's about the different ways you can order or rearrange these items. The order matters a lot in permutations. To find the number of permutations, you use the formula:

n!(n−r)!\frac{n!}{(n-r)!}(n−r)!n!

where:

  • nnn is the total number of items.
  • rrr is the number of items you are choosing and arranging.

In simple words, a permutation is a way to list all possible orders of a group of items.

Definition of Combination

A combination is when you select items from a group, but the order of the items doesn't matter. Unlike permutations, combinations don't care about the order of the items. To find the number of combinations, you use the formula:

n!r!(n−r)!\frac{n!}{r!(n-r)!}r!(n−r)!n!

where:

  • nnn is the total number of items.
  • rrr is the number of items you are choosing.

In combinations, the order of the selected items is not important. This concept is used in many areas like cryptography, statistics, and game theory.

Also Check:  4X4 Matrix Determinant | Determinant of Matrix | Determinants and Matrices | Diffrence Between Circle and Sphere

Permutation Formula

The formula for finding permutations is:

n!(n−r)!\frac{n!}{(n-r)!}(n−r)!n!

Here's what it means:

  • n!n!n! (n factorial) is the product of all positive numbers up to nnn. For example, 5!=5×4×3×2×1=1205! = 5 \times 4 \times 3 \times 2 \times 1 = 1205!=5×4×3×2×1=120.
  • This formula tells us how many different ways we can pick and arrange rrr items from a total of nnn items.

Combination Formula Explained in Simple Words

The combination formula helps us figure out how many ways we can pick a certain number of items from a larger group.

Here's the formula:

C(n,r)=n!r!⋅(n−r)!C(n, r) = \frac{n!}{r! \cdot (n - r)!}C(n,r)=r!⋅(n−r)!n!

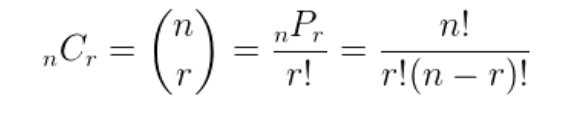
In this formula, "n" is the total number of items in a set, and "r" is the number of items you are picking from that set for the combination.

n! means the factorial of n, which is found by multiplying all whole numbers up to n. For example, 5! = 5 x 4 x 3 x 2 x 1 = 120.

r! means the factorial of r, which is found by multiplying all whole numbers up to r. For example, 3! = 3 x 2 x 1 = 6.

This formula helps you find the number of different ways to pick r items from a set of n items, without caring about the order.

Difference between Qualitative and Quantitative 

Difference Between Permutation and Combination

Permutation and combination are both ways to count items and find probabilities, but they are different:

  • Permutation cares about the order of the items.
  • Combination does not care about the order of the items.

Permutation

Combination

Arrangement of elements in a specific order

Selection of elements without regard to order

Order of elements is important

Order of elements is not important

Formula: n!/(n-r)!

Formula: n!/(r!(n-r)!)

Example: A permutation of the letters ABC is ABC, ACB, BAC, BCA, CAB, CBA

Example: A combination of the letters ABC is AB, AC, BC

Uses of Permutation and Combination

Permutation and combination are useful in many areas like math, computer science, cryptography, and statistics. Here are some common uses:

  1. Math: They help find the number of ways to arrange or combine items in a group.

  2. Computer Science: They are used in algorithms for pattern matching, coding, and securing data.

  3. Cryptography: These methods encode and decode messages to keep them safe.

  4. Statistics: They help calculate chances and figure out possible outcomes in experiments.

  5. Optimization: They solve problems in scheduling, resource sharing, and network planning.

Related Links

Frequently Asked Questions on Difference Between Permutation and Combination

When you arrange objects or letters in a specific order, it's called a permutation. But when you just pick a group of objects or letters without worrying about the order, that's a combination.

When you see words like selection, choose, pick, or combination, it means the question is about combinations. If you see words like arrangement, ordered, or unique, the question is about permutations.


 

The key difference between them is that permutations are groups where the order is important, while combinations are groups where the order doesn't matter. In permutation problems, you'll often see words like "arrangements," "lists," and "sequences."

Permutations are like arranging people, numbers, letters, or colors in a certain order. Combinations are like picking items for a menu, choosing food, clothes, subjects, or making a team.