Difference between Cube and Cuboid

We see many objects every day, like notebooks, matchboxes, geometry boxes, cones, cricket balls, and cylinders. These are all three-dimensional objects, or solid shapes. They have three dimensions: length, width, and height (or depth).

Some shapes have two or more faces that are the same (congruent). For example, a cube has square faces on each side, while a cuboid has rectangular faces on each side. A cube is a special type of cuboid with six faces, eight corners (vertices), and twelve edges. The cube’s sides are all equal in length, while a cuboid’s length, width, and height can be different. In this article, we'll talk about the definition, properties, and examples of cubes and cuboids. Keep reading to learn more.

Also Check:  4X4 Matrix Determinant | Determinant of Matrix  | Determinants and Matrices

Introduction

A cube and a cuboid are different mainly because a cube has six equal square faces, while a cuboid has rectangular faces. They share some features but differ in edge length, diagonals, and faces.

Shapes like cylinders, spheres, and cones have unique properties. However, cubes and cuboids share some common traits, such as having six faces, eight corners, and twelve edges. Also, all the inside angles are 90 degrees.

Cube

A cube is like a perfect square but in 3D. It looks like a box with six equal square faces. Each face meets another face at a 90-degree angle. Three sides of the cube come together at one corner.

Diffrence Between area and Volume

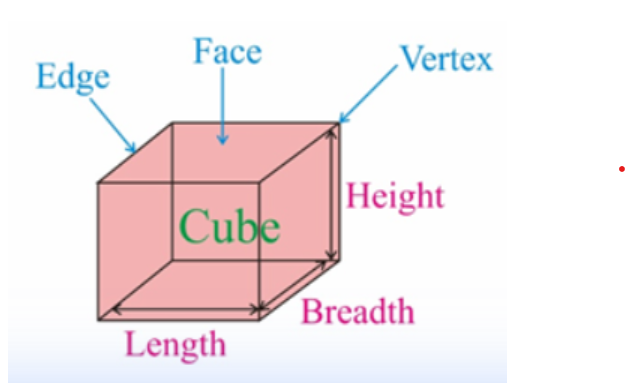
A cube has faces, edges, and corners, as shown in the picture. The cube has 8 corners, 12 edges, and 6 faces.

• Corners (Vertices): These are the 8 points where the edges meet.
• Edges: The 12 line segments that form the sides of the cube.
• Faces: The 6 flat square surfaces that make up the cube.

Faces of a Cube: These are the flat surfaces that make up the outside of the cube.

Edges of a Cube: These are the line segments where two faces come together.

Vertices of a Cube: These are the points where three faces meet.

Net a Cube

A net of a solid shape is a flat drawing you can cut out and fold to make that shape. For a cube, the net is a two-dimensional shape that you can fold into a 3D cube.

A cube has six square faces, twelve edges, and eight corners (vertices). When you unfold a cube and lay it flat, you get a two-dimensional shape called a net.

Diffrence Between Circle and Sphere

Formulas for a Cube

Lateral Surface Area of a Cube

A cube has edges of length 'a'. Each face of the cube is a square with an area of a2a^2a2.

So, the lateral surface area (the area of the 4 side faces) of the cube is:

Lateral Surface Area (LSA)=4a2 square units\text{Lateral Surface Area (LSA)} = 4a^2 \text{ square units}Lateral Surface Area (LSA)=4a2 square units

Total Surface Area of a Cube

A cube has 6 square faces. If each edge of the cube is 'a', then the total surface area of the cube is:

Total Surface Area (TSA)=6a2 square units\text{Total Surface Area (TSA)} = 6a^2 \text{ square units}Total Surface Area (TSA)=6a2 square units

Volume of a Cube

The volume of a cube is found by multiplying the edge length by itself three times. If each edge is 'a', then the volume is:

Volume (V)=a3 cubic units\text{Volume (V)} = a^3 \text{ cubic units}Volume (V)=a3 cubic units

Formulas for a Cuboid

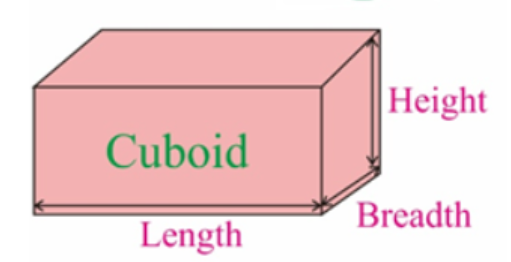
A cuboid is a box-like shape with three dimensions. It has 6 rectangular faces. Each face meets another face at a right angle (90 degrees). Three faces intersect at each vertex (corner).

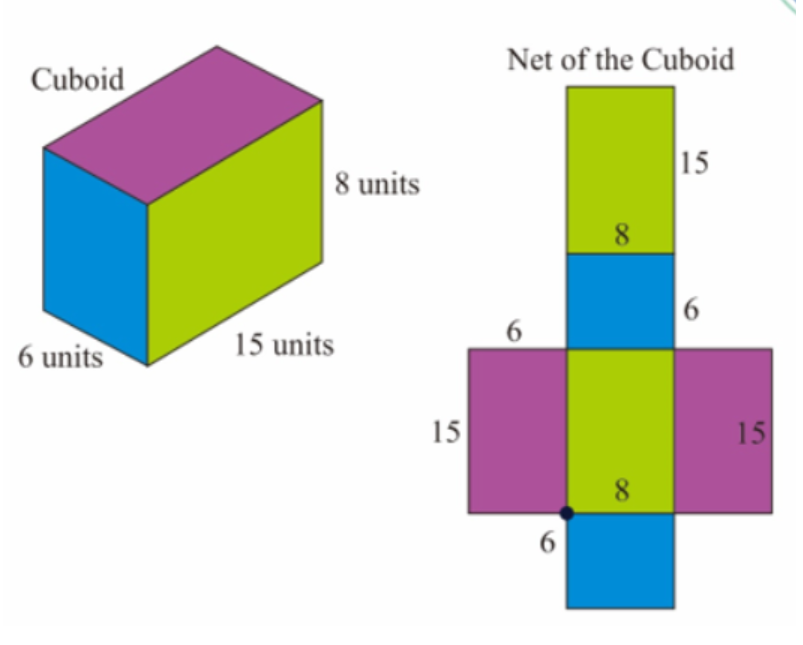
Net of a Cuboid

A cuboid has 6 rectangle faces, 12 edges, and 8 corners. When you unfold the rectangle faces and lay them flat, you get a 2D shape called a net of a cuboid. A cuboid looks like a rectangle-shaped shoe box.

Formulas of a Cuboid

Lateral Surface Area of a Cuboid
The lateral surface area is the sum of the four vertical sides of the cuboid.
LSA=2(l+b)h\text{LSA} = 2(l + b)hLSA=2(l+b)h
(square units)

Total Surface Area of a Cuboid
A cuboid has six rectangular faces. The total surface area is:
TSA=2(lb+bh+hl)\text{TSA} = 2(lb + bh + hl)TSA=2(lb+bh+hl)
(square units)
Where lll is length, bbb is breadth, and hhh is height.

Volume of a Cuboid
The volume is the space inside the cuboid:
V=l×b×hV = l \times b \times hV=l×b×h
(cubic units)

Difference Between a Cube and a Cuboid
A cube has all sides equal, while a cuboid has different lengths for length, breadth, and height.