Determinant of a Matrix

The determinant of a matrix is a single number that tells us important things about the matrix. It helps us understand if the matrix can be inverted, if its rows or columns are related, and its eigenvalues. In this article, we'll look at how to find the determinant for 1x1, 2x2, and 3x3 matrices. We'll also talk about minors and cofactors, and give examples for each size of matrix.

Also Check: 4X4 Matrix Determinant

Introduction

The concept of the determinant is one of the fundamental building blocks of linear algebra, and it is widely used in various fields such as physics, engineering, and computer graphics. It is a scalar value that can be calculated from a given square matrix and encodes important information about the matrix, such as its invertibility, orientation, and eigenvalues. In this article, we will explore the definition of the determinant of a matrix, how it can be calculated for various matrix sizes, and its properties and applications.

Definition of Determinant of Matrix

The determinant of a matrix is a scalar value that is calculated from the elements of a square matrix. It is a unique value for a given square matrix and is denoted by the symbol "det" or "| |". For example, the determinant of a matrix A can be represented as det(A) or |A|.

The determinant of a matrix is calculated using a specific formula, which depends on the size of the matrix. For a 2 × 2 matrix, the formula is given by:

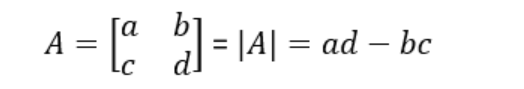
For larger matrices, calculating the determinant involves a more complex formula. It includes expanding the determinant along a row or column using minors and cofactors of the matrix elements.

Symbol:

The determinant of a matrix is often denoted by "det" or "| |". For instance, the determinant of matrix A is written as det(A) or |A|.

Determinant of a 1 × 1 Matrix: A 1 × 1 matrix, which is just a single number, has a determinant equal to that number itself. If A = (a), then the determinant |A| is simply equal to a. For example, if A = (3), then |A| = 3.

Determinant of a 2 × 2 Matrix: The determinant of a 2 × 2 matrix A = [[a, b], [c, d]] can be found using the formula |A| = ad - bc.

 

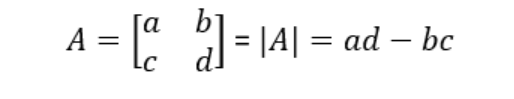
where, 

In other words, the determinant of a 2 × 2 matrix is equal to the product of its diagonal elements minus the product of its off-diagonal elements.

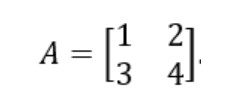
For example, if , then |A| = (1)(4) - (2)(3) = 4 - 6 = -2.

Minor of Element of a Matrix

The minor of an element in a matrix is found by taking the determinant of a smaller matrix. You get this smaller matrix by deleting the row and column that contain the element you're interested in.

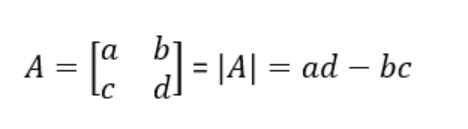
For instance, if you have a 2 × 2 matrix and you want the minor of element 'a', you remove its row and column, leaving a 1 × 1 matrix (denoted as 'd'). Then, the minor of 'a' is simply 'd'.

Co-factor of Element of a Matrix

The cofactor of an element in a matrix is determined by multiplying its minor (the determinant of the smaller matrix formed by removing the element's row and column) by the sign associated with its position in the matrix. The sign is positive if the element is in an even position and negative if it is in an odd position. For instance, in a 2 × 2 matrix like

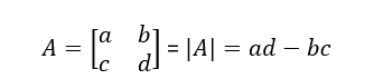
, the cofactor of element 'a' would be calculated as (-1)^(1+1) * ad = ad.'

Determinant of 3 × 3 Matrix

 

The determinant of a 3 × 3 matrix can be calculated using the rule of Sarrus, which involves adding and subtracting the products of elements along three diagonals. Alternatively, the determinant can be calculated by expanding along any row or column, using the minors and co-factors of the elements.

 

For example, if 

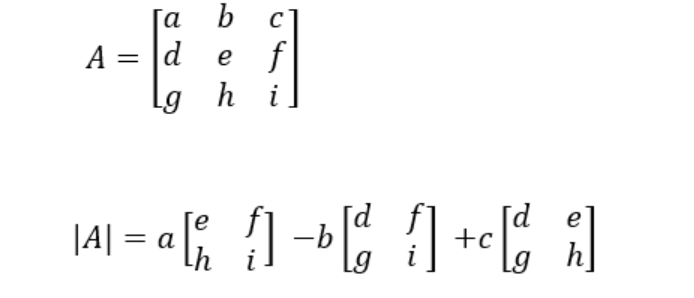
then,

where the minors of the elements are calculated using the determinant of the 2 × 2 matrices obtained by removing the corresponding row and column.

For example, if

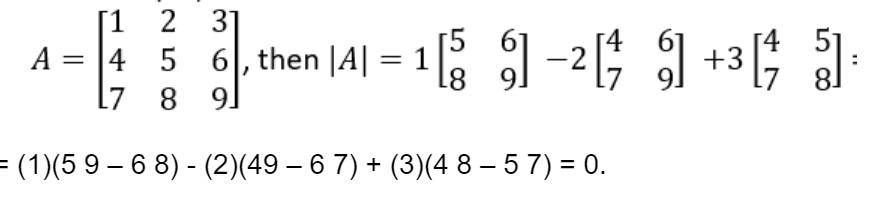
Determinant of larger matrices

The determinant of a matrix can be found for any square matrix, regardless of its size. As the matrix gets bigger, the method to find its determinant becomes more complex. For matrices larger than 3 × 3, people often use methods like LU decomposition or Gaussian elimination to calculate the determinant.

Properties and Applications of Determinant

The determinant of a matrix has many important uses in math, physics, engineering, and computer graphics. Here are some key things about it:

1. Invertibility: A matrix can be inverted (turned upside down) if its determinant isn't zero. If the determinant is zero, the matrix can't be inverted—it has no reverse version.

2. Orientation: The determinant tells us if a matrix keeps the same direction in space or flips it. If the determinant is positive, it keeps the direction; if negative, it flips the direction.

3. Eigenvalues: The determinant is linked to eigenvalues, which are numbers that describe how a matrix behaves. Specifically, the determinant equals the product of its eigenvalues.

 

Properties of Determinant of Matrix

Linearity: The determinant changes proportionally if you multiply a row or column of the matrix by a number. For example, if you double a row, the determinant doubles as well.

Multiplicativity: When you multiply two matrices together, their determinant equals the product of each matrix's determinant.

Invariance under row and column operations: Any operations that rearrange rows or columns without changing the matrix's essential structure do not alter its determinant.

Orthogonality: For orthogonal matrices, the determinant is either 1 or -1. This depends on whether you need an even or odd number of row swaps to turn the matrix into an identity matrix.

Singular matrices: A matrix is singular if its determinant is 0, which means it cannot be inverted.

Additivity: When dealing with block matrices, the determinant of the whole matrix is the sum of the determinants of its parts.

In conclusion, the determinant of a matrix is a single number that tells us important things about the matrix, like whether it can be inverted, its orientation, and its eigenvalues. Determinants are essential in many fields like math, physics, engineering, and computer graphics.