Students can use the cubes ranging from 1 to 50 to help them solve problems quickly. The cube of a number is the result of multiplying that number by itself three times.
Introduction to Cubes
When a number is multiplied three times, the resulting number is called the cube (x). In other words, the cube of a number (x) is x³ or x-cubed.For example, the cube of 3 is 3 × 3 × 3 = 27, which can be written as 3³ = 27. Any natural number raised to the power of three gives the cube of the original number.
What are Cubes?
Cubes are the values obtained by multiplying a number by itself three times. This can be done with both integers and fractions.The cube of a number (x) is x³ or x-cubed.
Perfect Cubes
A perfect cube is a number that can be written as the product of three identical or equal integers. For example, the number 125 is a perfect cube because 5 × 5 × 5 = 125. However, 121 is not a perfect cube because there is no integer that, when multiplied three times, gives 121.
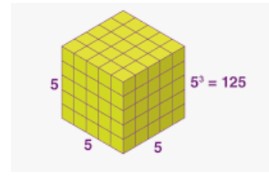
Cubed Numbers
To find the cube of a whole number (not a fraction), you can multiply the number by itself, and then multiply the result by the same number.For example, the cube of 5 can be written as 5³, which means 5 × 5 × 5 = 125.
Cube of Negative Numbers
The cube of a negative number will always be negative, while the cube of a positive number will always be positive.For example, the cube of -5 is -125, which can be written as -5³.By understanding the properties and applications of cubes, students can use the cubes ranging from 1 to 50 to solve problems more efficiently and gain a deeper understanding of mathematical concepts.
Cubes 1 to 50 table
|
Numberx |
Multiplied three times by itself |
Cubesx3 |
|
1 |
111 |
1 |
|
2 |
222 |
8 |
|
3 |
333 |
27 |
|
4 |
444 |
64 |
|
5 |
555 |
125 |
|
6 |
666 |
216 |
|
7 |
777 |
343 |
|
8 |
888 |
512 |
|
9 |
999 |
729 |
|
10 |
101010 |
1000 |
|
11 |
111111 |
1331 |
|
12 |
121212 |
1728 |
|
13 |
131313 |
2197 |
|
14 |
141414 |
2744 |
|
15 |
151515 |
3375 |
|
16 |
161616 |
4096 |
|
17 |
171717 |
4913 |
|
18 |
181818 |
5832 |
|
19 |
191919 |
6859 |
|
20 |
202020 |
8000 |
|
21 |
212121 |
9261 |
|
22 |
222222 |
10648 |
|
23 |
232323 |
12167 |
|
24 |
242424 |
13824 |
|
25 |
252525 |
15625 |
|
26 |
262626 |
17576 |
|
27 |
272727 |
19683 |
|
28 |
282828 |
21952 |
|
29 |
292929 |
24389 |
|
30 |
303030 |
27000 |
|
31 |
313131 |
29791 |
|
32 |
323233 |
32768 |
|
33 |
333333 |
35937 |
|
34 |
343434 |
39304 |
|
35 |
353535 |
42875 |
|
36 |
363636 |
46656 |
|
37 |
373737 |
50653 |
|
38 |
383838 |
54872 |
|
39 |
393939 |
59319 |
|
40 |
404040 |
64000 |
|
41 |
414141 |
68921 |
|
42 |
424242 |
74088 |
|
43 |
434343 |
79507 |
|
44 |
444444 |
85184 |
|
45 |
454545 |
91125 |
|
46 |
464646 |
97336 |
|
47 |
474747 |
103823 |
|
48 |
484848 |
110592 |
|
49 |
494949 |
117649 |
|
50 |
505050 |
125000 |
Division Method to Find the Cube Root
The division method is analogous to the long division method or the manual square method for obtaining the cube root. Make a set of three-digit numbers from the back to the front. The next step is to find a number that has a cube root that is less than or equal to the supplied integer.
Subtract the obtained number from the specified number and enter the result in the second box. Then, multiply the initial number obtained to obtain the multiplication factor for the next step in the long division procedure. Repeat the above procedure to find the cube root of a number. This lengthy division method is used when the given integer is not a perfect cube number. This method takes a long time to find the cube root of an integer.
Frequently Asked Questions
Learning the cubes from 1 to 50 is beneficial for students as it helps them quickly solve problems involving cube calculations. Having a reference for the cubes of numbers from 1 to 50 allows students to perform complex calculations more efficiently without the need for a calculator or extensive computations.
The cube of a number is calculated by multiplying the number by itself three times. For example, the cube of 4 is 4 × 4 × 4 = 64, which can be written as 4³.
A perfect cube is a number that can be expressed as the product of three identical integers. For example, 27 is a perfect cube because it can be written as 3 × 3 × 3 = 27.
The cube of a negative number will always be negative, while the cube of a positive number will always be positive. For instance, the cube of -5 is -125, while the cube of 5 is 125.