Total Surface Area of Cube
Total Surface Area of Cube
The surface area of a cube refers to the combined area of all six of its square faces. To find this, we calculate the area of each of the two square bases and then add the areas of the four square lateral sides. A cube is a three-dimensional geometric figure composed entirely of square faces. Understanding its surface area is essential for tasks such as wrapping the cube or painting its surfaces effectively.
Also Check: Total Surface Area of Hemisphere
What is the Surface Area of a Cube?
The surface area of a cube equals the combined area of its bases and lateral surfaces. Each face of a cube is a square of identical dimensions. Therefore, the total surface area of a cube is calculated by multiplying the area of one face by six, as a cube has six faces. The measurement unit for surface area could be square centimeters, square inches, square feet, etc. There are two types of surface area that can be calculated for a cube: the area of its lateral surfaces alone, and the total surface area which includes all six faces.
- Area of lateral surface
- Surface area total
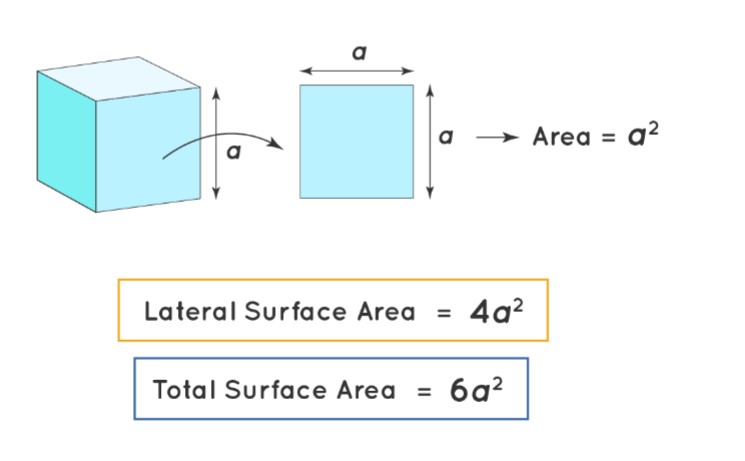
Total Surface Area (TSA) of a Cube
The Total Surface Area of a cube refers to the combined area of all six of its faces. This includes the area of each square face summed together to give the total external coverage of the cube.
Lateral Surface Area (LSA) of a Cube
The Lateral Surface Area of a cube specifically pertains to the total area of its side faces. To calculate the LSA, we sum the areas of these four rectangular faces. This measurement excludes the areas of the top and bottom faces, focusing solely on the sides that form the outer shell of the cube.
Surface Area of a Cube Formula
The surface area of a cube, which measures the total area that its six faces cover, depends on its edge length. Here's how we calculate both the total and lateral surface areas:
Total Surface Area of a Cube Formula
The total surface area of a cube is found by multiplying the square of its edge length by 6.
Formula: Total Surface Area = 6 × side2 square units
Lateral Surface Area of a Cube Formula
The lateral surface area of a cube considers only the area of its four side faces.
Formula: Lateral Surface Area = 4 × side2 square units
How to Find the Surface Area of a Cube?
The total surface area of a cube can be found by multiplying the square of its side length by 6. To calculate this, multiply the side length by itself (square it), and then multiply the result by 6
- Measure the Edge Length: Start by measuring the length of one side of the cube.
- Square the Edge Length: Calculate the square of this measured length.
- Calculate Surface Areas:
- For Total Surface Area: Multiply the squared side length by 6.
- For Lateral Surface Area: Multiply the squared side length by 4.
- Write Your Answer: Provide your solution in square units, which represents the total or lateral surface area of the cube.
Understanding these formulas and steps helps in accurately determining how much surface area a cube covers based on its dimensions.
Related Links
- Derivative of Inverse Trigonometric functions
- Decimal Expansion Of Rational Numbers
- Cos 90 Degrees
- Factors of 48
- De Morgan’s First Law
- Counting Numbers
- Factors of 105
- Cuboid
- Cross Multiplication- Pair Of Linear Equations In Two Variables
- Factors of 100
- Factors and Multiples
- Derivatives Of A Function In Parametric Form
- Factorisation Of Algebraic Expression
- Cross Section
- Denominator
- Factoring Polynomials
- Degree of Polynomial
- Define Central Limit Theorem
- Factor Theorem
- Faces, Edges and Vertices
- Cube and Cuboid
- Dividing Fractions
- Divergence Theorem
- Divergence Theorem
- Difference Between Square and Rectangle
- Cos 0
- Factors of 8
- Factors of 72
- Convex polygon
- Factors of 6
- Factors of 63
- Factors of 54
- Converse of Pythagoras Theorem
- Conversion of Units
- Convert Decimal To Octal
- Value of Root 3
- XXXVII Roman Numerals
- Continuous Variable
- Different Forms Of The Equation Of Line
- Construction of Square
- Divergence Theorem
- Decimal Worksheets
- Cube Root 1 to 20
- Divergence Theorem
- Difference Between Simple Interest and Compound Interest
- Difference Between Relation And Function
- Cube Root Of 1728
- Decimal to Binary
- Cube Root of 216
- Difference Between Rows and Columns
- Decimal Number Comparison
- Data Management
- Factors of a Number
- Factors of 90
- Cos 360
- Factors of 96
- Distance between Two Lines
- Cube Root of 3
- Factors of 81
- Data Handling
- Convert Hexadecimal To Octal
- Factors of 68
- Factors of 49
- Factors of 45
- Continuity and Discontinuity
- Value of Pi
- Value of Pi
- Value of Pi
- Value of Pi
- 1 bigha in square feet
- Value of Pi
- Types of angles
- Total Surface Area of Hemisphere
- Total Surface Area of Cube
- Thevenin's Theorem
- 1 million in lakhs
- Volume of the Hemisphere
- Value of Sin 60
- Value of Sin 30 Degree
- Value of Sin 45 Degree
- Pythagorean Triplet
- Acute Angle
- Area Formula
- Probability Formula
- Even Numbers
- Complementary Angles
- Properties of Rectangle
- Properties of Triangle
- Co-prime numbers
- Prime Numbers from 1 to 100
- Odd Numbers
- How to Find the Percentage?
- HCF Full Form
- The Odd number from 1 to 100
- How to find HCF
- LCM and HCF
- Calculate the percentage of marks
- Factors of 15
- How Many Zeros in a Crore
- How Many Zeros are in 1 Million?
- 1 Billion is Equal to How Many Crores?
- Value of PI
- Composite Numbers
- 100 million in Crores
- Sin(2x) Formula
- The Value of cos 90°
- 1 million is equal to how many lakhs?
- Cos 60 Degrees
- 1 Million Means
- Rational Number
- a3-b3 Formula with Examples
- 1 Billion in Crores
- Rational Number
- 1 Cent to Square Feet
- Determinant of 4×4 Matrix
- Factor of 12
- Factors of 144
- Cumulative Frequency Distribution
- Factors of 150
- Determinant of a Matrix
- Factors of 17
- Bisector
- Difference Between Variance and Standard Deviation
- Factors of 20
- Cube Root of 4
- Factors of 215
- Cube Root of 64
- Cube Root of 64
- Cube Root of 64
- Factors of 23
- Cube root of 9261
- Cube root of 9261
- Determinants and Matrices
- Factors of 25
- Cube Root Table
- Factors of 28
- Factors of 4
- Factors of 32
- Differential Calculus and Approximation
- Difference between Area and Perimeter
- Difference between Area and Volume
- Cubes from 1 to 50
- Cubes from 1 to 50
- Curved Line
- Differential Equations
- Difference between Circle and Sphere
- Cylinder
- Difference between Cube and Cuboid
- Difference Between Constants And Variables
- Direct Proportion
- Data Handling Worksheets
- Factors of 415
- Direction Cosines and Direction Ratios Of A Line
- Discontinuity
- Difference Between Fraction and Rational Number
- Difference Between Line And Line Segment
- Discrete Mathematics
- Disjoint Set
- Difference Between Log and Ln
- Difference Between Mean, Median and Mode
- Difference Between Natural and whole Numbers
- Difference Between Qualitative and Quantitative Research
- Difference Between Parametric And Non-Parametric Tests
- Difference Between Permutation and Combination
Frequently Asked Questions on Total Surface Area of Cube
The Total Surface Area (TSA) of a cube is the sum of the areas of all six faces. The formula for the TSA of a cube is 6a^2, where 'a' is the length of one side. The Curved Surface Area (CSA) or Lateral Surface Area (LSA) of a cube is the combined area of the four side faces, which is 4a^2.
To find the surface area of a cube, you need to know the length of one side. Then, you can use the formula 6a^2 to calculate the Total Surface Area (TSA) of the cube, where 'a' is the side length. The Lateral Surface Area (LSA) is calculated as 4a^2.
The formula for the Total Surface Area (TSA) of a cube is 6a^2, where 'a' is the length of one side of the cube. This formula represents the sum of the areas of all six faces of the cube.
The Lateral Surface Area (LSA) or Curved Surface Area (CSA) of a cube is the combined area of the four side faces, excluding the top and bottom faces. The formula for the LSA of a cube is 4a^2, where 'a' is the length of one side.
The Total Surface Area (TSA) of a cube is the sum of the areas of all six faces of the cube. The formula for the TSA of a cube is 6a^2, where 'a' is the length of one side. This represents the total area that covers the outside of the cube.