Prime Numbers from 1 to 100

1 to 100 Prime Numbers

Prime numbers are defined by having exactly two factors: 1 and the number itself. Take the number 5, for instance, which has only two factors: 1 and 5. This characteristic qualifies it as a prime number. Conversely, consider the number 6, which has more than two factors: 1, 2, 3, and 6. Therefore, 6 does not meet the criteria for being a prime number.

Another aspect to consider is the number 1, which has only one factor, itself. This single factor disqualifies it from being categorized as a prime number, as prime numbers must possess exactly two factors. In mathematical classification, 1 stands alone as neither prime nor composite, distinguishing it as a unique number.

What Are Prime Numbers?

A prime number is a natural number greater than one that has exactly two distinct positive divisors: one and itself. Essentially, a prime number cannot be evenly divided by any other number except one and itself. For instance, the number 7 cannot be divided into equal parts because it can only be expressed as a product of 1 and 7:

  • 7 × 1 = 7
  • 1 × 7 = 7

Prime numbers

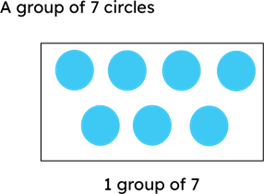
Number 7 consists solely of the digits 1 and 7, making it a prime number because it cannot be divided evenly by any other number.

A prime number is defined as a whole number greater than one that can only be divided evenly by 1 and itself.

History of Prime Numbers

In ancient times, prime numbers sparked fascination among scholars. Today, mathematicians continue to pursue prime numbers with unique characteristics. Euclid's theorem asserts that there is an endless supply of prime numbers.

To identify prime numbers up to a given number, n, we generate a list of integers from 2 to n. Beginning with the smallest prime, p = 2, we eliminate all multiples of 2 except 2 itself from the list. This process continues with the next prime number, progressively larger than 2.

List of Prime Numbers

Here is the list of Prime numbers from 1 to 100:

List of Numbers Prime Numbers
From 1 - 10 2, 3, 5, 7
From 11 - 20 11, 13, 17, 19
From 21 - 30 23, 29
From 31 - 40 31, 37
From 41 - 50 41, 43, 47
From 51 - 100 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Related Links

Frequently Asked Questions on Prime Numbers from 1 to 100