Differential calculus is a part of math focused on finding the derivative of a function. It studies how quantities change in relation to other variables. Finding a function's derivative is called differentiation.
Introduction Calculus and Approximation
Differential calculus is a part of mathematics focused on finding a function's derivative. It examines how quantities change in relation to other variables. The process of finding a derivative is called differentiation. Essentially, differential calculus involves breaking things down to see how they change.
A differential equation involves the derivative of a dependent variable with respect to an independent variable, such as dydx = f(x), where x is the independent variable and y is the dependent variable.
Also Check: Difference Between Variance and Standard Deviation
Derivatives are useful for:
- Calculating the rate of change of quantities.
- Finding the equations of tangent and normal lines to a curve at a point.
- Identifying turning points on a graph to find maximum or minimum values.
- Determining intervals where a function increases or decreases.
- Estimating approximate values of various quantities.
For example, to find the rate of change of a circle's area (A = πr2) with respect to its radius (r) when r is 5 cm:
dA/dr = d/dr(πr2) = 2πr
When r = 5 cm:
dA/dr = 2π × 5 = 10π
Differential Calculus Approximations
Differentials can approximate quantities. Let f(x) be a function. If x increases by a small amount Δx, the corresponding change in y is Δy = f(x + Δx) - f(x) as illustrated in the figure below.
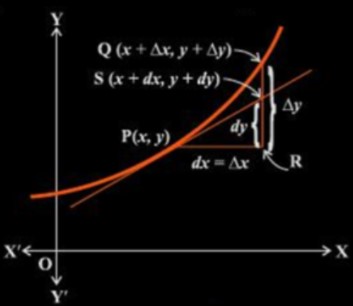
Based on the previous discussion:
- The differential of x, denoted as dx, is dx = x.
- The differential of y, denoted as dy, is dy = f'(x)dx = (dy/dx)x.
- If dx is very small compared to x, then dy closely approximates y.
Also Check: Difference Between Variance and Standard Deviation
Example of Differential Calculus and Approximation
To approximate 25.5 using a differential:
- Let y = x, where x = 25 and dx = 0.5.
Then,
- dy = f'(x)dx = 1 × 0.5 = 0.5.
So, the approximate value of 25.5 is:
- 25 + 0.5 = 25.5.
Conclusion
Differential calculus helps calculate how one quantity changes in relation to another. The rate of change of x relative to y is denoted by dx/dy. It is a key concept in calculus alongside integrals.
Frequently Asked Questions
Approximation by differentials is a method to estimate the value of a function near a known point using the tangent line at that point. It involves using the derivative to calculate the change in the function.
In calculus, an approximation is a simplified expression that estimates the value of a function or quantity. It provides a close estimate without calculating the exact value.
In calculus, a differential represents an infinitesimal change in a variable. The differential of the independent variable (dx) can be assigned any small value, while the differential of the dependent variable (dy) is defined as dy = f'(x)dx.
Differential calculus is the study of rates of change using derivatives. It can be used to optimize functions by finding the maximum or minimum values. Optimization involves finding the best solution among various alternatives.
The approximation formula in calculus is f(x+Δx) ≈ f(x) + f'(x)Δx, where f(x) is a function, Δx is a small change in the independent variable x, and f'(x) is the derivative of f(x). This formula provides an estimate of the function value near.