Decimal number comparison is the process of determining which of two decimal numbers is greater or smaller. Decimal numbers are numbers with one or more digits after the decimal point, such as 0.75, 1.23, or 2.5.
Comparing decimal numbers is a fundamental mathematical operation used in many applications, such as ordering or sorting values and making mathematical decisions based on the relative size of numbers.
There are two main methods for comparing decimal numbers:
- The Graphical Method
- The Analytical Method
Decimal Number Comparison using Graphical Method
The graphical method of comparing decimal numbers involves representing the numbers on a number line. To use this method:
- Draw a number line with evenly spaced tick marks.
- Label one end of the number line with the smaller number and the other end with the larger number.
- Place both numbers on the number line.
- Determine which number is to the right or left of the other.
- The number to the right is greater and the number to the left is smaller.
For example, if you wanted to compare 0.75 and 0.5, you would draw a number line and place 0.75 on one end and 0.5 on the other. Since 0.75 is to the right of 0.5, you would conclude that 0.75 is greater than 0.5.
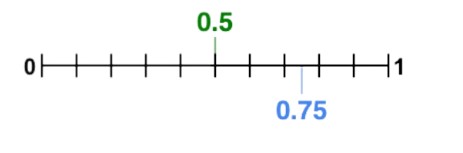
Decimal Number Comparison Example using Graphical Method
Let's compare the decimal numbers 0.6 and 0.58.
- Draw the number line with evenly spaced tick marks.
- Label one end of the number line with 0.58 and the other end with 0.6.
- Place both numbers on the number line.
- Observe which number is to the right or left of the other.
- In this case, 0.6 is to the right of 0.58.
So, using the graphical method, we have determined that 0.6 is greater than 0.58.
Decimal Number Comparison using Analytical Method
The analytical method of comparing decimal numbers involves comparing each place value of the numbers, starting from the rightmost digit and moving left. To use this method:
- Write down both numbers.
- Starting from the rightmost digit, compare the corresponding place values of the two numbers.
- If one number has a greater value in a particular place value, it is the larger number.
- If the place values are equal, move to the next place value and continue comparing.
- If all place values are equal, the numbers are equal.
For example, if you wanted to compare 0.75 and 0.73, you would write down both numbers and compare the hundredths place values (75 and 73). Since 75 is greater than 73, you would conclude that 0.75 is greater than 0.73.
Decimal Number Comparison Example using Analytical Method
Let's compare the decimal numbers 0.6 and 0.58.
- Write down both numbers: 0.6 and 0.58.
- Starting from the rightmost digit, compare the corresponding place values of the two numbers.
- In this case, the hundredths place values are 60 and 58.
- Since 60 is greater than 58, we can conclude that 0.6 is greater than 0.58.
So, using the analytical method, we have determined that 0.6 is greater than 0.58.
Frequently Asked Questions
There are two main methods for comparing decimal numbers: The Graphical Method And the Analytical Method
The graphical method involves representing the numbers on a number line, while the analytical method involves comparing each place value of the numbers, starting from the rightmost digit and moving left.
The analytical method is faster for comparing decimal numbers because it does not require drawing a number line.
Yes, the graphical method can be used for larger decimal numbers, but it may require a more complex number line. The analytical method can also be used for larger decimal numbers and is not limited by the size of the numbers.
The graphical method is best used when visualizing the relationship between numbers is helpful, such as when teaching the concept to students or for simple comparison problems.