100 million in Crores

100 million in Crores:When dealing with large numbers, it’s essential to understand the different numeral systems used around the world. In this blog, we will explore the conversion of 100 million into crores, and delve into the nuances of both the Indian and International number systems. By breaking down these systems, we will see how they are used in different contexts and clarify how large numbers are represented and understood.

What is 100 Million in Crores?

Let’s start with a simple question: How do you convert 100 million into crores? To answer this, we need to understand the basic relationship between these two units of measurement.

In the Indian number system:

1 Crore is equivalent to 10,000,000 (10 million).
Therefore, 100 Million is equal to 10 Crores.

Calculation: 100,000,000(100 million)÷10,000,000;(1 crore)=10 crores

The Indian Number System: A Detailed Overview

The Indian numeral system is unique and commonly used in South Asia. It structures numbers differently from the International system. Let’s break it down:

Understanding Place Values

In the Indian number system, the place values for a number like 10,23,45,678 are:

8 – Ones
7 – Tens
6 – Hundreds
5 – Thousands
4 – Ten Thousand
3 – Lakhs
2 – Ten Lakhs
1 – Crores
This system groups numbers in lakhs and crores. For example:

1 Lakh = 1,00,000
10 Lakhs = 10,00,000
1 Crore = 1,00,00,000

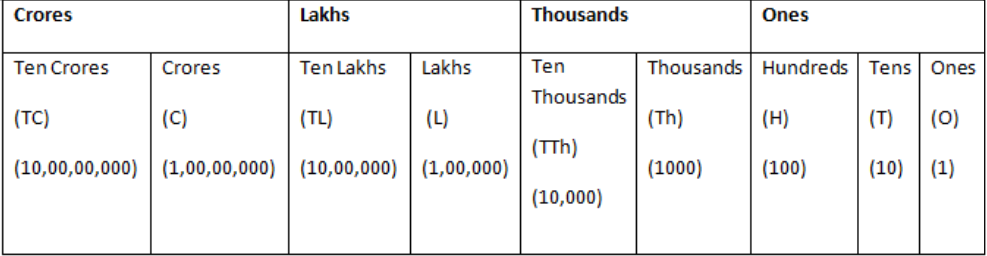
The Indian system uses these terms to simplify large numbers, which helps in financial transactions and general communication.

The International Number System: An Overview

The International numeral system is used worldwide and has a different structure from the Indian system. Here’s a breakdown of the place values for a number like 12,34,56,78:

8 – Ones
7 – Tens
6 – Hundreds
5 – Thousands
4 – Ten Thousand
3 – Hundred Thousand
2 – Millions
1 – Ten Million
The International system uses terms like thousands, millions, and billions. For instance:

1 Million = 1,000,000
10 Million = 10,000,000
100 Million = 100,000,000

Converting Between Million and Crore

To convert between the International and Indian numeral systems, we need to recognize the equivalent terms:

1 Million = 10 Lakhs
1 Crore = 10 Million
100 Million = 10 Crores
Example Conversion:
If you have 100 Million dollars, it converts to 10 Crores in the Indian system. This conversion is straightforward since both systems use different groupings but represent the same values.

Real-World Applications of Crores and Millions

Understanding these conversions is not just an academic exercise; it has practical applications in various fields:

1. Finance and Economics
In finance, large sums of money are often discussed in millions or crores. For example, multinational corporations might report revenues in millions of dollars, while Indian companies might report their earnings in crores.

2. Government Budgets
Government budgets and expenditures are typically reported in crores in India. For instance, the annual budget might be presented as several thousand crores, which can be converted to millions for international comparisons.

3. Business Transactions
Businesses involved in international trade might need to convert between these units when negotiating contracts or reporting financials to international stakeholders.

Common Misconceptions About Million and Crore

There are a few common misconceptions when it comes to understanding these numerical terms:

1. Misunderstanding the Size
Some people might confuse a crore with a million, thinking they are similar, but a crore is 10 times larger than a million.

2. Confusion Between Systems
People might mix up the Indian and International systems, especially in contexts like financial reports or international transactions. Understanding both systems can help avoid such confusion.

Conclusion

Navigating between millions and crores involves more than just mathematical conversion—it requires understanding the different numeral systems and their applications. Whether you are dealing with international finance or local budgets, knowing how to convert and interpret these numbers is crucial.