NCERT Class 5 Maths Chapter 11 Area and Its Boundary

NCERT Solutions Chapter 11 Area and Its Boundary

NCERT Solutions for Class 5 Maths Chapter 11 Area and Its Boundary of the NCERT textbook is solved with errorless solutions by experts on Home-tuition.com. Chapter 11 Area and Its Boundary is fully solved in the below pdf. You can download a chapter-wise free pdf of Chapter 11 Area and Its Boundary.

What are you going to learn in Chapter 11 Area and Its Boundary?

Area and its Boundary-Paras and Gini bought cheese slices from a shop. Both could not make out whose piece was bigger. They wanted some ways to find out whose piece is bigger. A friend of Paras and Gini showed one way, using small squares. Another way is to visually compare but to find a concrete method to understand the concept of area and perimeter we will study in this chapter.

Paras and Gini bought cheese slices from a shop. Both could not make out whose piece was bigger. They wanted some ways to find out whose piece is bigger. A friend of Paras and Gini showed one way, using small squares. Another way is to visually compare but to find a concrete method to understand the concept of area and perimeter we will study this chapter

Find below a free pdf of NCERT Solutions for Class 5 Maths Chapter 11 Area and Its Boundary

Page No 146:

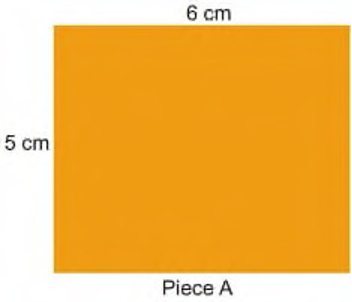
Question 1: Parth and Gini bought aam paapad (dried mango slice) from a shop. Their pieces looked like these.

Both could not make out whose piece was bigger.

• Suggest some ways to find out whose piece is bigger. Discuss. A friend of Parth and Gini showed one way, using small squares.

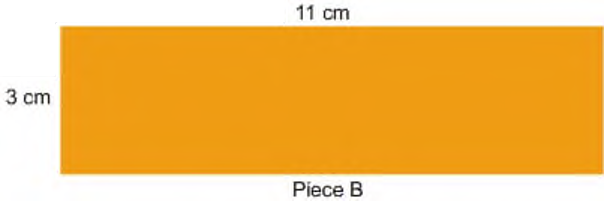
The length of piece A is 6 cm. So 6 squares of side 1 cm can be arranged along its length. The width of piece A is 5 cm. So 5 squares can be arranged along its width.

• Altogether how many squares can be arranged on it?__________

• So the area of piece A = _____________square cm

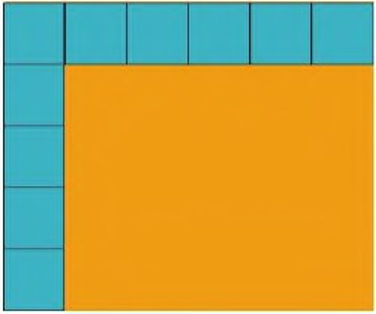
• In the same way find the area of piece B.

• Who had the bigger piece? How much bigger?

Answer:

The length of piece A is 6 cm. So, 6 squares of side 1 cm can be arranged along its length.

The width of piece A is 5 cm. So, 5 squares can be arranged along its width.

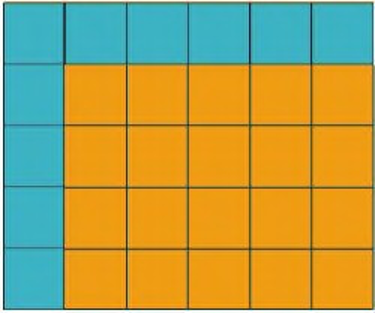
• Altogether 30 squares can be arranged on it.

• So, the area of piece A = 6 cm × 5 cm = 30 square cm

• Now, the area of piece B = 11 cm × 3 cm = 33 square cm

• So, the area of piece B is bigger than the area of piece A. Difference in area of piece A and piece B = 33 square cm − 30 square cm = 3 square cm

So, piece B is 3 square cm bigger than piece A.

Page No 147:

Question 1: This stamp has an area of 4 square cm. Guess how many such stamps will cover this big rectangle.

Answer:

An approximate of 27 stamps will cover this big rectangle.

Disclaimer: The answer may vary from student to student, based on his/her observation. It is highly recommended that the students prepare the answer on their own. The answer provided here is for reference only.

Page No 148:

Question 1:

Check your guess

(a) Measure the yellow rectangle. It is _________cm long.

(b) How many stamps can be placed along its length? _______

(c) How wide is the rectangle?__________cm

(d) How many stamps can be placed along its width?____________

(e) How many stamps are needed to cover the rectangle?____________

(f) How close was your earlier guess? Discuss.

(g) What is the area of the rectangle?___________ square cm

(h) What is the perimeter of the rectangle? _________cm

Answer:

(a) The yellow rectangle is 14 cm long.

(b) Measure the length of stamp already placed on it with the help of a ruler. Length of stamp = 2 cm. So, the required number of stamps =

Length of rectangle / Length of stamp = 14/2 = 7

Thus, we can place 7 stamps along the length of the rectangle.

(c) The breadth of yellow rectangle is 8 cm.

(d) Measure the width of stamp placed along its width with the help of a ruler. Width of stamp = 2 cm So, the required number of stamps =

Breadth of rectangle / Breadth of stamp = 8/2 = 4

Thus, we can place 4 stamps along the breadth of the rectangle.

(e) The number of stamps that can be placed in the rectangle = 7 ×4 = 28

(f) Our guess for the stamp was 27, but the actual answer is 28. So, we can say that our guess was quite close to the correct answer.

(g) Area of rectangle = 7 cm × 4 cm = 28 square cm The area of rectangle is 28 square cm.

(h) Length of the rectangle = 14 cm Breadth of the rectangle = 8 cm A rectangle has 2 lengths and 2 breadths.

So, perimeter of the rectangle = Sum of all its sides = Length of its boundary = 14 cm + 8 cm + 14 cm + 8 cm = 44 cm

The perimeter of rectangle is 44 cm.

Question 2: Arbaz plans to tile his kitchen floor with green square tiles. Each side of the tile is 10 cm. His kitchen is 220 cm in length and 180 cm wide. How many tiles will he need?

Answer:

Length of kitchen = 220 cm

Each side of tile = 10 cm

Number of tiles that can be placed along its length =

Length of kitchen / Length of each tile = 220/10 = 22

Breadth of kitchen = 180 cm Length of each side of tile = 10 cm

Number of tiles that can be placed along its breadth =

Breadth of kitchen / Breadth of each tile = 180/10 = 18

Number of tiles that he will need for kitchen = 22 × 18 = 396

Question 3: The fencing of a square garden is 20 m in length. How long is one side of the garden?

Answer:

Length of the fencing of square garden = 20 m We know that a square has 4 sides and all its sides are equal.

So, length of each side of a square =

Length of fencing of garden / Number of sides of a square = 20/4 = 5m

Question 4:

A thin wire 20 centimetres long is formed into a rectangle. If the width of this rectangle is 4 centimetres, what is its length?

Answer:

We know that a rectangle has two equal lengths and two equal widths. Now, width of a rectangle = BC = AD = 4 cm Sum of the two widths of rectangle = 4 cm + 4 cm =8 cm

Also, length of rectangle = AB = CD So, we get the remaining length of rectangle = 20 cm − 8 cm = 12 cm

Now, we know a rectangle has two lengths and they are equal. So, we divide it by 2 to get the length. Length of rectangle = 12/2 cm = 6 cm

Page No 149:

Question 1: A square carrom board has a perimeter of 320 cm. How much is its area?

Answer:

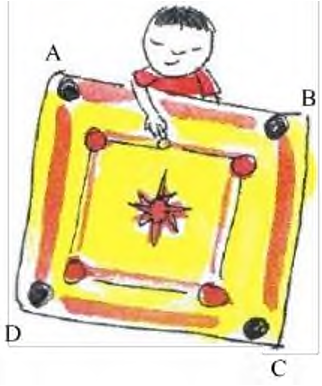
As the carrom board is square, so length of all its sides will be equal. Side

= AB = BC = CD = AD Therefore, its perimeter = sum of all its sides = 320 cm

Now, all the 4 sides are equal, so we divide 320 by 4. Thus, length of each side = 320/4 cm = 80 cm

Now, area of a square carrom board = side × side = 80 cm × 80 cm = 6400 square cm

Question 2: How many tiles like the triangle given here will fit in the white design? Area of design =____________square cm

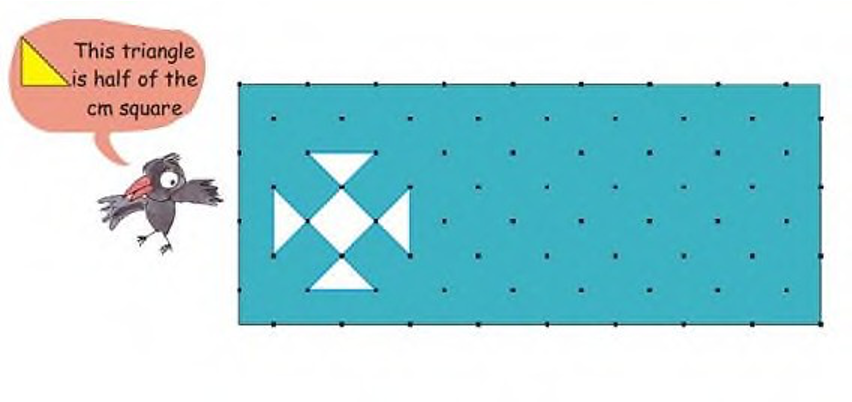
Answer:

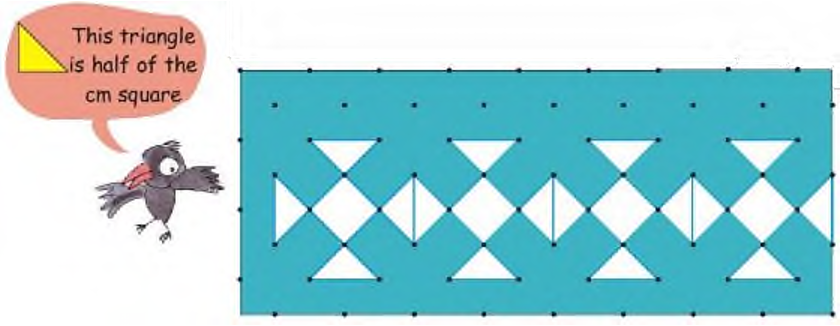
6 triangular tiles will fit in to the given white design. Now, area of 1 such triangular tile = 12 square cm Area of 6 triangular tiles that make this design = 6 × 12 = 3 square cm Area of design = 3 square cm

Question 3: Sanya, Aarushi, Manav and Kabir made greeting cards. Complete the table for their cards:

Whose card	Length	Width	Perimeter	Area
Sanya	10 cm	8 cm
Manav	11 cm		44 cm
Aarushi		8 cm		80 square cm
Kabir			40 cm	100 square cm

Answer:

Perimeter of Sanya’s card = Sum of all its sides = 10 + 8 + 10 + 8 = 36 cm

Length of Manav’s card = 11 cm Perimeter of his card = 44 cm We have to find the width of Manav’s card.

Perimeter of card = Sum of all its sides = 11 + 11 + sum of 2 other sides

= 22 + sum of 2 other sides

Now, sum of two other sides = 44 − 22 = 22 cm The two other sides of the greeting cards are width. So, width of Manav’s card = 22 ÷ 2 = 11 cm

Width of Aarushi’s card = 8 cm Area of the card = 80 square cm Now, we have to find length of the card.

Area of card = Length of card × 8 cm = 80 square cm So, on dividing the area of card by its width, we can get its length. Therefore, length of Aarushi’s card = 80 ÷ 8 = 10 cm

Whose card	Length	Width	Perimeter	Area
Sanya	10 cm	8 cm	36 cm	80 square cm
Manav	11 cm	11 cm	44 cm	121 square cm
Aarushi	10 cm	8 cm	36 cm	80 square cm
Kabir	10 cm	10 cm	40 cm	100 square cm

Question 4: Take a thick paper sheet of length 14 cm and width 9 cm. You can also use an old postcard.

• What is its area? What is its perimeter?

• Now cut strips of equal sizes out of it.

Using tape join the strips, end to end, to make a belt.

• How long is your belt?__________

• What is its perimeter___________

• Whose belt is the longest in the class?___________

Answer:

Length of paper sheet = 14 cm Breadth of paper sheet = 9 cm Area of the sheet = 14 cm × 9 cm = 126 square cm

Perimeter of the sheet = 14 cm + 9 cm + 14 cm + 9 cm = 46 cm

Disclaimer: The answer may vary from student to student. It is highly recommended that the students prepare the answer on their own.

Page No 151:

Question 1: Make two squares of one square metre each. Divide your class in two teams. Ready to play! Try these in your teams —

• How many of you can sit in one square metre? ___________

• How many of you can stand in it?___________

• Which team could make more children stand in their square? How many?___________

• Which team could make more children sit in their square? How many?

Answer:

Disclaimer: The purpose of this section is to make students carry this activity and observe their results. The answer may vary from student to student, based on his/her experience. It is highly recommended that the students prepare the answer on their own.

Question 2: Measure the length of the floor of your classroom in metres. Also measure the width.

• What is the area of the floor of your classroom in square metres?_____

• How many children are there in your class?___________

• So how many children can sit in one square metre? ___________

• If you want to move around easily then how many children do you think should be there in one square metre?___________

Answer:

Disclaimer: The purpose of this section is to make students observe their surroundings. The answer may vary from student to student, based on his/her experience. It is highly recommended that the students prepare the answer on their own.

Page No 152:

Question 1: Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.

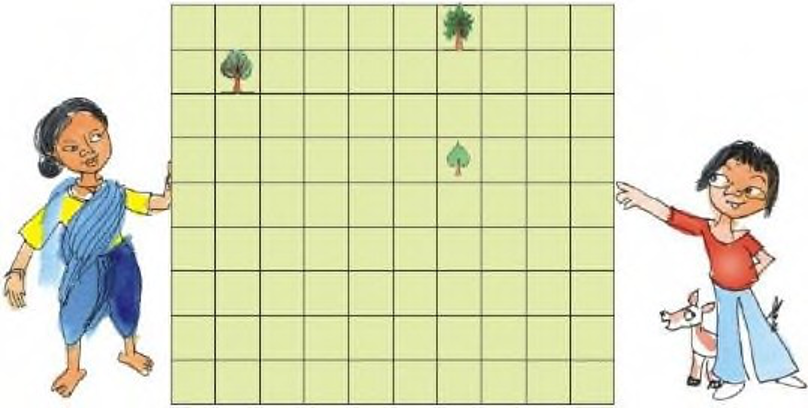
• Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.

• If each square on this page is equal to 1 square metre of land, how much land will each of her children get? _____________square m Chumki, Jhumri and Imran need wire to make a fence.

• Who will need the longest wire for fencing? ________

• How much wire in all will the three need?__________

Answer:

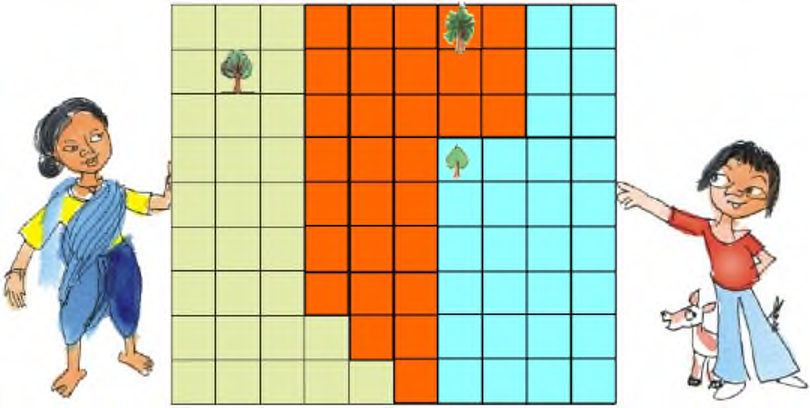
There are 10 squares along the length, and 9 squares along the width. So, the total number of squares on the land = 10 × 9 = 90 Now, area of each square = 1 square m So, area of complete land = area of 90 squares = 90 ×1 square m = 90 square m

Nasreena has 3 children namely Chumki, Jhumri and Imran, and she divides her land equally among her children. So, area of land each child

gets = 90/3square m = 30 square m

• Both Chumki and Jhumri will need 28 m of wire for fencing.

• Imran will need 26 m of wire for fencing his part of the field. Thus, total wire required by all three of them = 28 + 28 + 26 = 82 m

Page No 153:

Question 1: Look at the table. If you were to write the area of each of these which column would you choose? Make a ().

	Square cm	Square metre	Square km
Handkerchief	
Sari
Page of your book
School land
Total land of a city
Door of your classroom
Chair seat
Blackboard
Indian flag
Land over which a river flows

Answer:

	Square cm	Square metre	Square km
Handkerchief	
Sari		
Page of your book	

School land			
Total land of a city			
Door of your classroom		
Chair seat	
Blackboard		
Indian flag	
Land over which a river flows			

Page No 154:

Question 1: Draw a square of 9 square cm. Write A on it. Draw another square with double the side. Write B on it. Answer these — 1. The perimeter of square A is__________cm. 2. The side of square B is ___________cm. 3. The area of square B is ________square cm. 4. The area of square B is_______times the area of square A. 5. The perimeter of square B is_________cm. 6. The perimeter of square B is________times the perimeter of square A.

Answer:

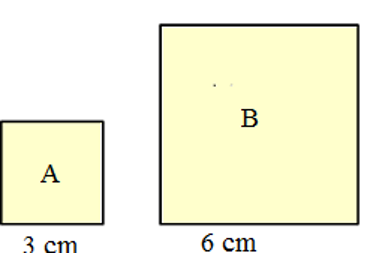
1. Each side of square A = 3 cm So, perimeter of square A = Sum of all its sides = 3 + 3 + 3 + 3 = 12 cm

2. Each side of square B = Double the side of square A So, side of square B = 2 × length of side of square A = 2 × 3 = 6 cm

3. Area of square B = 6 × 6 = 36 square cm

4. Area of square A = 3 × 3 = 9 square cm So, area of square B is 4 times the area of square A.

5. Perimeter of square B = Sum of all its sides = 6 + 6 + 6 + 6 = 24 cm Perimeter of square B is 2 times the perimeter of square A.

Page No 155:

Question 1: Take a 15 cm long thread. Make different shapes by joining its ends on this sheet.

(A) Which shape has the biggest area? How much? _______What is the perimeter of this shape? ________

(B) Which shape has the smallest area? How much?________ What is the perimeter of this shape? _______Also make a triangle, a square, a rectangle and a circle. Find which shape has biggest area and which has the smallest.

Answer:

Disclaimer: The purpose of this section is to make students perform this activity and observe the results. The answer may vary from student to student, based on his/her experience. It is highly recommended that the students prepare the answer on their own.

Page No 156:

Question 1: There are two beautiful lakes near a village. People come for boating and picnics in both the lakes. The village Panchayat is worried that with the noise of the boats the birds will stop coming. The Panchayat wants motor boats in only one lake. The other lake will be saved for the birds to make their nests.

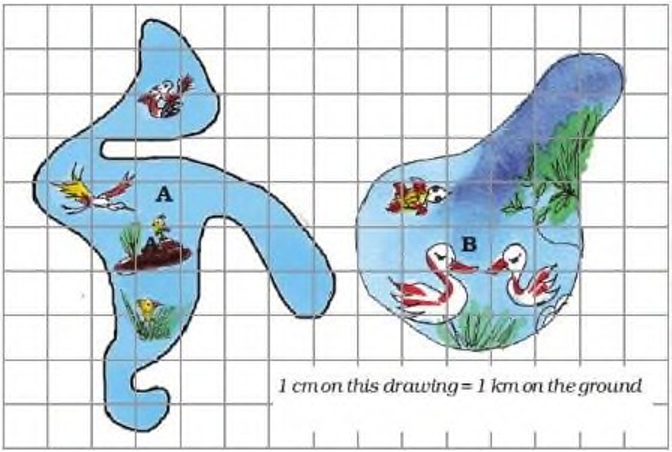
(a) How many cm is the length of the boundary of lake A in the drawing?____________(use thread to find out)

(b) What is the length of the boundary of lake B in the drawing?

(c) How many kilometres long is the actual boundary of lake A?

(d) How many kilometres long is the actual boundary of lake B?

(e) A longer boundary around the lake will help more birds to lay their eggs. So which lake should be kept for birds? Which lake should be used for boats?

(f) Find the area of lake B on the drawing in square cm. What is its actual area in square km?

Answer:

(a) When we measure the boundary of lake A with the help of thread, it comes out to be around 30 cm.

(b) When we measure the boundary of lake B with the help of thread, it comes out to be around 25 cm.

(c) Here, the scale is 1 cm = 1 km So, length of the actual boundary of lake A = 30 km

(d) Here, the scale is 1 cm = 1 km So, length of the actual boundary of lake B = 25 km

(e) The boundary around the lake A is more than the boundary around the lake B. So, lake A should be kept for birds and lake B should be used for boats.

(f) Lake B has 15 fully filled squares and 11 half-filled or more than half

– filled squares. Area of 15 fully filled squares = 15 × 15 = 225 square cm

We consider the area of every single half – filled or more than half – filled square as 1 centi metre square.

Thus, the area of 11 such squares = 11 × 11 = 121 square cm So, total area of lake B = 225 + 121 = 346 square cm

We are given 1 cm on drawing = 1 km on ground Therefore, 346 square cm on drawing = 346 km

Page No 157:

Question 1: The King was very happy with carpenters Cheggu and Anar. They had made a very big and beautiful bed for him. So as gifts the king wanted to give some land to Cheggu, and some gold to Anar. Cheggu was happy. He took 100 metres of wire and tried to make different rectangles. He made a 10 m × 40 m rectangle. Its area was 400 square metres. So he next made a 30 m × 20 m rectangle.

• What is its area? Is it more than the first rectangle?

What other rectangles can he make with 100 metres of wire? Discuss which of these rectangles will have the biggest area. Cheggu’s wife asked him to make a circle with the wire. She knew it had an area of 800 square metres.

• Why did Cheggu not choose a rectangle? Explain. So Anar also tried many different ways to make a boundary for 800 square metres of land.

• He made rectangles A, B and C of different sizes. Find out the length of the boundary of each. How much gold wire will he get for these rectangles?

A

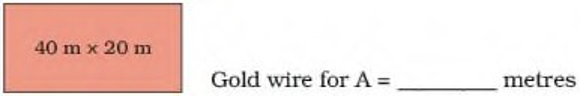
B

C

But then Anar made an even longer rectangle…… See how long!

D

So he will get _________metres of gold wire!!

Answer:

Area of 30 m × 20 m rectangle = 600 square metres Its area is larger than the area of first rectangle.

The other rectangles that he can make with 100 metres of wire are 40 m × 10 m, 48 m × 2 m, 49 m × 1 m, 45 m × 5 m

A

As the area of rectangle A is shown as 40 m × 20 m. So, the length of rectangle = 40 m Width of rectangle = 20 m

Gold wire for A = 40 + 20 + 40 + 20 = 120 metres

B

As the area of rectangle B is shown as 80 m ×10 m. So, the length of rectangle = 80 m Width of rectangle = 10 m

Gold wire for B = 80 + 10 + 80 + 10 = 180 metres

C

As the area of rectangle C is shown as 800 m ×1 m. So, the length of rectangle = 800 m Width of rectangle = 1 m

Gold wire for C = 800 + 1 + 800 + 1 = 1602 metres

D

As the area of rectangle D is shown as 8000 m × 0.1 m. So, the length of rectangle = 8000 m Width of rectangle = 0.1 m Gold wire for C = 8000

+ 0.1 + 8000 + 0.1 = 16000 + 0.2 = 16000.2 metres. So, he will get 16000.2 metres of gold wire!!