NCERT Class 4 Maths Chapter-12 How Heavy? How Light?

NCERT Solutions for Class 4 Maths Chapter-12

NCERT textbook consists of Chapter 12 How Heavy? How Light? which consists of lots of questions in exercise as well as inside the textbook, our experts solved all the questions asked in Tables And Shares as per the CBSE guideline.

What are you going to learn in Chapter 12 How Heavy? How Light?

This chapter starts with Jaiju and Mannu shifting house. Both of them are shifting house while shifting house They loaded all their things on a horse-cart. Lots of things are in the house having different weight shapes and like a water tank, three tables, an almirah, four chairs, two mattresses, five sacks of wheat, three sacks of rice, a bamboo ladder, pots and pans.

During this activity, they understood the use of weight. This chapter tells you all information required to find the weight including the units of weight like kg. you will find the following

A sack of wheat 100 kg

A sack of rice 35 kg

Water tank 50 kg

Almirah 70 kg

A table 10 kg

A chair 5 kg

A mattress 20 kg

Bamboo ladder 10 kg

Pots and pans 10 kg

Download step-by-step explanation of NCERT Solutions for Chapter 12 How Heavy? How Light?

1. Father gave them some idea of the weight of each thing.

Find out the total weight they had loaded on the cart. Now they decided to remove a few things from the cart.

Which things should be removed so that the weight of the load is not more than 700 kgs?

Ans: The things loaded on the cart are and their weights are: 5 sacks of wheat = 5 x 100kg = 500kg

3 sacks of rice = 3 x 35kg = 105kg

1 water tank = 1 x 50kg = 50kg

1 Almirah = 1 x 70kg = 70kg

3 Tables = 3 x 10kg = 30kg

4 ChaiRs = 4 x 5kg = 20kg

2 Mattresses = 2 x 20kg = 40kg

1 Bamboo ladder = 1 x 10kg = 10kg

1 Pot and pan = 1 x 10kg = 10kg

The total weight of the things loaded is equal to the sum of the weights of the individual thing.

Therefore the total weight of the things loaded is

500 +105 +10 + 50 + 70 + 30 + 20 + 40 +10 +10 = 845 kg

The total weight of things loaded = 845 kg.

The extra weight is 845 - 700 = 145 kg .

For the weight of the load is not more than 700 kg, We need to remove 145 kg from the load.

A sack of wheat + A sack of rice + A table = 100 + 35 +10 = 145 kg

So we can remove a sack of wheat, rice and a table from the load so that the weight of the load will not be more than 700 kg.

2. Now you also make your own balance. Write down how you made it. Also draw a picture of your balance in the box below.

Ans: Steps to make a balance:

1. Take a Symmetrical rod.

2. Now take two similar wires and tie it at both the end of the rod.

3. Take two similar pans and hang the plate with the help of the rod.

4. Now place the hook at the centre of the symmetrical rod.

3. Activity Mannu and Jaiju put a pencil and a geometry box in the two pans of the balance. Which pan will go down? Why? Draw a picture to show it.

Ans: The pan which has a geometry box will go down because the geometry box is heavier than a pencil.

4. What is heavier? Make pair of different things and use the balance to decide which is heavier. First guess which thing will take the pan down and then check with your balance.

Ans: Let us make a pair of geometry boxes and a pencil. As we know that a geometry box is always heavier than a pencil, it will take the pan down.

5. What is the heaviest? Make groups of three things. For example - eraser, ball and paper. Use the balance to arrange them in order of weight – the lightest, the one within–between weight, the heaviest. Complete the table with at least five examples.

Can you find your own weight using this balance?

Ans:

Balance is invented to find which is heavier given two objects, so we cannot find our own weight using this balance.

6.Practice Time

Which pan of the balance will go down? Show by drawing an arrow. Is the weight on any of the pans equal to 1 kilogram? Mark it.

(a)

Ans: In the above diagram the left pan has 65g and the right pan has 75g, so the right pan will go down.

(b)

Ans: In the above diagram the left pan has 150g and the right pan has 175g so the right pan will go down.

(C)

Ans: In the above diagram the left pan has 300g and the right pan has 400g, so the right pan will go down

(d)

Ans: In the above diagram the left pan has 1000g and the right pan has 854g, so the left pan will go down.

(e)

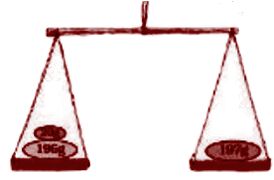
Ans: In the above figure the load in the left pan is higher than the load in the right pan, so the left pan will go down.

(f)

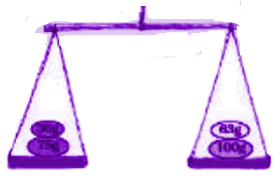
Ans: In the above diagram the right pan has heavier load than the right, so the right pan will go down.

Yes, the 4^th diagram has 1000g in the left pan which is equal to 1kg.

7.Grams and Kilograms Name 5 things that we usually buy.

Ans: In grams we buy things which are required in very less quantity whereas in kg we buy things which are required in large quantities.

8.Guess and write the weight of each thing he bought in g or kg.

Ans: Rice, Sugar, Wheat are bought in kg because it weighs heavier and mustard seeds, dal, tea and pepper are bought in g.

9.Now you show how Abdu will use these stone pieces to weigh.

(a)4 kg of firewood

Ans: Abdu can place 6kg stone in one pan and 2kg stone along with firewood on another pan. Once the weights of both the pans are equal then he can say that the weight of the firewood is 4kg.

(b)

3 kg of firewood

Ans: Abdu can place 5 kg stones on one pan and 2 kg of stone along with firewood on the other pan. If the weight of both the pan is equal then, he can say that the weight of firewood is 3kg.

(c)7 kg of firewood

Ans: Abdu can place a 5kg and 2kg stone on one pan and firewood on the other pan. If both the pans become equal in weight, he can say that the firewood weighs 7kg.

10. Post Office Have you ever been to a post office? __What different things do people go there for? How much does a postcard cost?_____How much does an inland letter cost?______

Ans: Yes, I have been to the post office twice with my mother.

People go there to post and collect telegrams, letters etc. A postcard usually costs one or two rupees.

An inland letter costs 3 Rupees.

11.The following rate list is given.

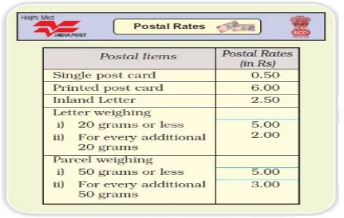
Look at the postal rates given in the chart.

11.1.How much will you have to pay for stamps on a letter weighing 50 grams?________

Ans: It is given that for 20 or less the postal rates are 5 Rs. And for every additional 20g the postal rate is 2 Rs.

50g = 20g + 20g +10g

So, the stamp rate for the 50g letter = 5 + 2 + 2 = 9

The total rate paid for the stamps = 9 Rs.

11.2.Akash wants to send a parcel of the Math Magic textbook to his friend Rani in Chennai. The book weighs 200 g. See the chart to find the cost of posting the book. ___

Ans: We know that the weight of the book is 200g.

200g = 50g + 50g + 50g + 50g

The cost for the parcel weighing less than or equal to 50g is 5Rs and for every additional 50g the cost is 3Rs.

Thus, the cost of the parcel = (5 +3 +3 +3) =Rs 14

The cost for posting the book is 14 Rs.

12.Read the weight shown in the picture. Find out the cost of sending a parcel of that weight.

Parcel weight =_______ Cost of stamps = ________ .

Ans: The total weight of the parcel is 230 g .

The cost of a 50 g parcel is Rs5 and for every extra 50g the cost is Rs3.

230g = 50g + 50g + 50g + 50g + 30g

 

Thus, the cost of the stamps = Rs(5 +3+3+3+3)

= Rs.17

Thus the total cost of a parcel weighing 230g is 17 rupees. Parcel weight = 230g

Cost of stamps = 17Rs.

13.How Many Stamps?

Rahul needs stamps of Rupees 25 for his parcel. He went to the post office. Only stamps of Rs1, Rs2, Rs5 and Rs10 were there at that time. Using those stamps in how many different ways can he make Rs25?

Can you show five different ways? What is the heaviest parcel he can send using stamps of Rs 25?

Ans: The 5 different ways are shown below:

i.5 stamps of Rs 5

= 5 x 5

= Rs 25

ii. 1 stamp of 5 Rupees and 2 stamps of 10 rupees

= 1 x 5 + 2 x 10

= 5 + 20

= Rs. 25

iii. 10 stamps of Rs 2 each and 1 stamp of Rs 5.

= 10 x 2 + 1 x 5

= 20 + 5

= Rs. 25

iv. 3 stamps of Rs 5 each and 5 stamps of Rs 2.

= 3 x 5 + 2 x 5

= 15 +10

= Rs 25

v. 3 stamps of Rs 5 each and 1 stamp of Rs 10

= 3 x 5 +1 x 10

= 15 +10

= Rs 25

14. Our Weight Together: A frog was struggling to escape from the mouth of a crow. How can I escape? The frog thought. Suddenly a trick came to his mind. He asked the crow Are you good at arithmetic? If yes, then I will ask you a problem.

Your weight is 650 g and I am only 145 g. How much do we weigh together?

The crow was good at mathematics, so he sappily opened his beak to answer. What happened after that? So what was the answer the crow wanted to give?________

 

Ans:

 

The weight of the crow = 650 g The weight of the frog = 145 g

The weight of the crow and the frog together = 650g +145g = 795g

The crow happily said the answer was 795g and when the crow opened the mouth the frog escaped from the crow’s mouth.

15.Now, you also fill the table by finding out the age, height and weight of any five friends.

Ans: Let us take five friends whose names are Anoop, Taufeeq, Harish, Sattheesh, Suresh.

Enter the age, height and weight as you wish.

Q16. How Many Oranges? All oranges have equal weight. The two papayas have the same weight. The weights in the first and second balances are equal. How many oranges balance the weight in the third?

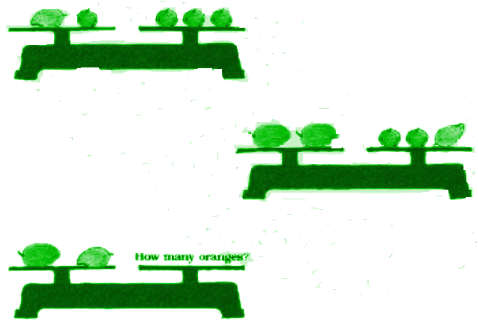
Ans: In the first balance there is an orange and a papaya in the left pan and 3 oranges in the right pan.

We can understand that

1 orange + 1 Mango = 3 oranges Removing 1 orange from both the sides, 1 Mango = 2 orange

From the 2^nd balance,

2 papaya = 2 oranges + 1 mango We know that 1 mango = 2 orange 2 papaya = 4 oranges

i.e. 1 papaya = 2 orange From the 1^st and 2^nd balance, 1 mango = 2 orange

1 papaya = 2 orange So,1 mango = 1 papaya

In the 3^rd balance there is 1 mango and 1 papaya in the left pan

i.e. 1 mango + 1 papaya = 2 orange + 2 oranges = 4 oranges

Thus, to balance the weight in the third image, 4 oranges need to be placed.

17. Find That Marble: There are 3 marbles of the same size but one marble is slightly heavier or lighter than the other two. Can you find which is that marble and if it is heavier or lighter? You can use a balance only two times.

Ans: If there are 2 marbles of same weight and 1 marble slightly heavier or lighter than the other two then we can find out which marble is slightly different in the following ways:

Step 1: Name the marbles as x, y, z.

Step 2: Place x on one pan and y on the other. Case 1: Both the marble weighs the same Case 2: The marble x is heavier than marble y. Case 3: The marble y is heavier than marble x.

step 3 of case 1: If both the marble weighs the same then that means marble x and y are of same weight and the weight of marble z is different. To find if marble z is heavier or lighter remove marble x and place marble z. If marble z is heavier than x then the third marble is heavier and if it weighs lighter than the third marble is lighter.

Step 3 for case 2: In this case marble z is either equal to marble x or marble y. To find out, remove marble x (heavier) and place marble z against marble y (lighter).

There can be two cases again

Case 1- Marble z can be equal to marble y. This means both marble y and z are of equal weight and marble x is heavier

Case 2- Marble z can be heavier than marble y. This means marble z and marble x are the same and marble y is lighter than the other two.

Step 3 for case 3: In this case the marble x and y can be renamed. The heavier marble can be renamed as x and the lighter can be renamed as y. Now, to find out the weight of marble z. Repeat step 3 for case 2.