General

Distance Time Graphs – Part 2

By User
On

Distance–time graph for non-uniform motion

We already know that for a uniform motion, the distance-time graph is a straight line. This is because a body in uniform motion covers equal distances in equal intervals of time.

Now if a body is undergoing non-uniform motion, the body covers unequal distances in equal intervals of time. This makes the distance-time graph non-linear.

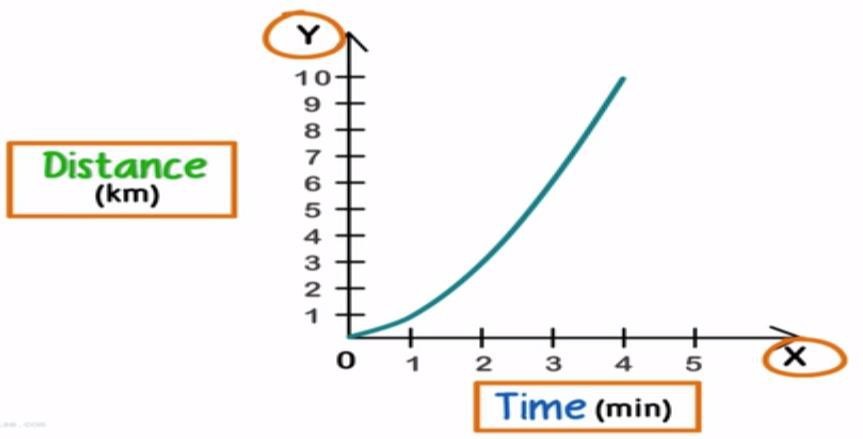
Distance-time graph for non-uniform motion

Distance-time graph for non-uniform motion

How to find the distance traveled by a body in non-uniform motion?

To find the distance traveled by the body at any time instant, we will mark a point corresponding to that time on the X-axis, on the graph. Mapping this point towards the Y-axis, we can find the distance travelled by that body.

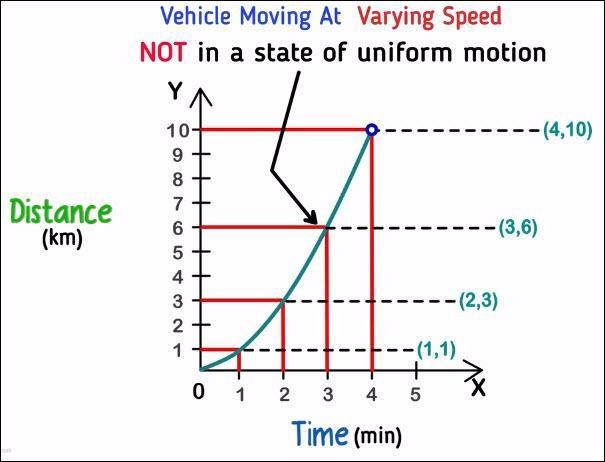
Non-uniform motion example

Non-uniform motion example

From this graph, we can say that distance travelled by the vehicle in 1 minute is 1 kilometer, in 2 minutes it is 3 kilometers, in 3 minutes it is 6 kilometers and so on.

How to find the speed of a body in non-uniform motion?

Using the same graph as above, let us calculate the speed of the vehicle at 4 minutes.

Being a non-linear graph, we cannot find the slope of this graph. To calculate the speed of a body in non-uniform motion, all we need to do is apply the formula of speed for that instant of time.

From the graph, we can see that 4 minute on the X-axis corresponds to 10 kilometers on the Y- axis.

Substituting the values, we get,

𝑆𝑝𝑒𝑒𝑑 =10 𝑘𝑚/4 𝑚𝑖𝑛

=2.5 x km/min

This speed is not the constant speed of that vehicle in non-uniform motion, but the variable speed calculated at that instant of time.

Related Posts:

  1. What is the difference between uniform and nonuniform motion?
  2. What is the difference between linear and logistic regression?
  3. Define uniform and non uniform motion.
  4. What is the difference between uniform linear motion and uniform circular motion? Explain with examples.
  5. Light travels in a straight line
  6. AAS (or SAA) test : The sum of the measures of angles in a triangle is . Therefore, if two corresponding pairs of angles in two triangles are congruent, then the remaining pair of angles is also congruent. Hence, if two angles and a side adjacent to one of them are congruent with corresponding parts of the other triangle then the condition for ASA test is fulfilled. So the triangles are congruent. List the other such tests to prove the congruence of triangles.