Share
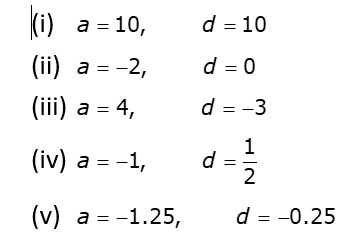
Question
- Here, first term a1 = 10 and common difference, d = 10
Hence,
2nd term a2 = a1 + d
= 10 + 10
= 20
3rd term a3 = a1 + 2d
= 10 + 2 x 10
= 30
4th term a4 = a1 + 3d
= 10 + 30
= 40
Therefore,
first four terms of the AP are:
10, 20, 30, 40, ……
- Here,
First term a = 1 and Common difference = 0
Therefore, first four terms of the given AP are:
a1 = - 2, a2 = - 2, a3 = - 2 and a4 = - 2
- Here, first term a1 = 4 and common difference d = - 3
We know that an = a + (n – 1)d, where n = number of terms
Thus, second term a2 = a + (2 – 1)d
a2 = 4 + (2-1)×(-3)
= 4 - 3 = 1
3rd term a3 = a + (3 – 1)d
= 4 + (3-1) × (-3)
= 4 - 6
= -2
4th term a4 = a + (4-1)d
= 4 + (4 - 1) ×( -3)
= 4 - 9 = -5
Therefore,
First four terms of given AP are:
4, 1, - 2, - 5
- We have,
1st term = - 1 and d = ½
Hence,
2nd term a2 = a1 + d
= -1 + ½
= - ½
3rdterm a3 = a1 + 2d
= -1 + 2 * ½
= 0
4th term a4 = a1 + 3d
= -1 + 3 * ½
= ½
Therefore,
The four terms of A.P. are -1, - ½, 0, ½
- We have
1st term = - 1.25 and d = - 0.25
2nd term a2 = a + d
= -1.25 - 0.25
= -1.5
3rd term a3 = a + 2d
= -1.25 + 2 × (-0.25)
= -1.25 - 0.5
= -1.75
4th term a4 = a + 3d
= 1.25 + 3 × (-0.25)
= -2.25
Therefore, first four terms of the A.P. are: 1.25, -1.5, -1.75 and – 2.25
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply