Share
or a non-terminating repeating decimal expansion:
(i)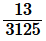
(ii)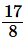
(iii)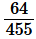
(iv)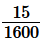
(v)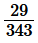
(vi)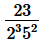
(vii)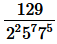
(viii)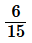
(ix)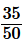
(x)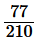
Question
(i)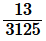
Factorize the denominator we get,
3125 = 5×5×5×5×5 = 55
The denominator is of the form 5m
Hence, the decimal expansion of is terminating.
(ii)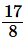
Factorize the denominator we get,
8 = 2 × 2 ×2 = 23
The denominator is of the form 2m
Hence, the decimal expansion of is terminating.
(iii)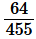
Factorize the denominator we get,
455 = 5×7×13
Since, the denominator is not in the form of 2m × 5n, and it also contains 7 and 13 as its factors,
Its decimal expansion will be non-terminating repeating.
(iv)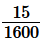
Factorize the denominator we get,
1600 = 26×52
The denominator is in the form 2m × 5n
Hence, the decimal expansion of is terminating.
(v)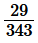
Factorize the denominator we get,
343 = 73
Since the denominator is not in the form of 2m × 5n, it has 7 as its factors.
So, the decimal expansion of non-terminating repeating.
(vi)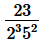
The denominator is in the form 2m×5n
Hence, the decimal expansion of is terminating.
(vii)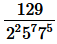
Since, the denominator is not in the form of 2m × 5n, as it has 7 in denominator.
So, the decimal expansion of is non-terminating repeating.
(viii)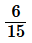
The denominator is in the form 5n
Hence, the decimal expansion of is terminating.
(ix)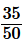
Factorize the denominator we get,
10 = 2×5
The denominator is in the form 2m×5n
Hence, the decimal expansion of is terminating.
(x)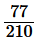
Factorize the denominator we get,
30 = 2×3×5
Since the denominator is not in the form of 2m × 5n, as it has 3 in denominator.
So, the decimal expansion of is a non-terminating repeating.
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply