Share
find it by using cross multiplication method.
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii)2x + y = 5
3x + 2y = 8
(iii) 3x − 5y = 20
6x − 10y = 40
(iv) x − 3y – 7 = 0
3x − 3y – 15 = 0
Report
Question
(i) x − 3y – 3 = 0
3x − 9y – 2 = 0
Comparing equation x − 3y – 3 = 0 with a1x +b1y + c1 = 0 and 3x − 9y – 2 = 0 with a2x +b2y + c2 = 0,
We get,
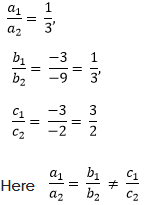
Therefore, the given sets of lines are parallel to each other. Therefore, they will not intersect each other and thus, there will not be any solution for these equations.
2x + y = 5
3x + 2y = 8
Comparing equation 2x + y -5= 0 with a1x +b1y + c1 = 0 and 3x + 2y -8= 0 with a2x +b2y + c2 = 0,
We get,
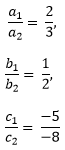
Here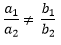 this means that there is unique solution for the given equations.
this means that there is unique solution for the given equations.
By cross-multiplication method,
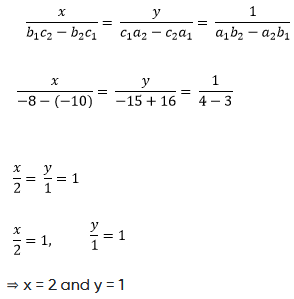
3x − 5y = 20
6x − 10y = 40
Comparing equation 3x − 5y = 20 with a1x +b1y + c1 = 0 and 6x − 10y = 40 with a2x +b2y + c2 = 0 ,
We get
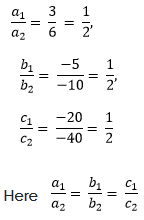
It means lines coincide with each other.
Hence, there are infinite many solutions.
(iv) x − 3y – 7 = 0
3x − 3y – 15 = 0
Comparing equation x − 3y – 7 = 0 with a1x +b1y + c1 = 0 and 3x − 3y – 15 = 0 with a2x +b2y + c2 = 0,
We get,
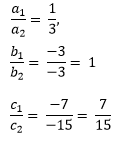
Here 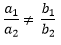 this means that we have unique solution for these equations.
this means that we have unique solution for these equations.
By cross-multiplication,
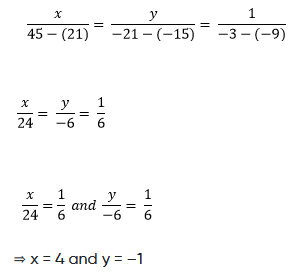
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply