Share
(i) The value of tan A is always less than 1
(ii) 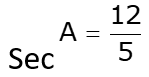 for some value of angle A
for some value of angle A
(iii) Cos A is the abbreviation used for the cosecant of angle A
(iv) Cot A is the product of cot and A.
(v) 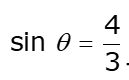 for some angle θ
for some angle θ
Report
Question
(i) Consider a ΔABC, right-angled at B
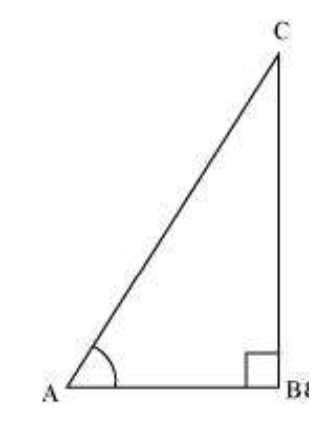
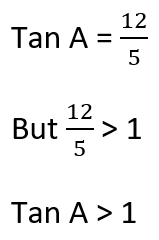
So, Tan A < 1 is not always true
Hence, the given statement is false
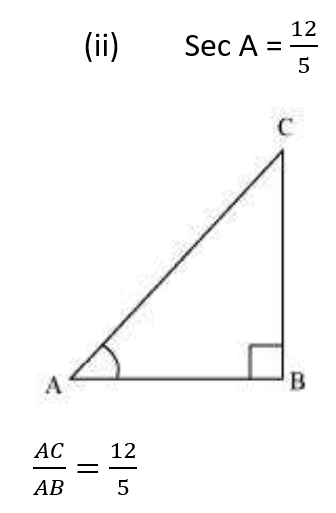
Let AC be 12k, AB will be 5k, where k is a positive integer
Applying Pythagoras theorem in ΔABC, we obtain
AC2 = AB2 + BC2
(12k)2 = (5k)2 + BC2
144k2 = 25k2 + BC2
BC2 = 119k2
BC = 10.9k
It can be observed that for given two sides AC = 12k and AB = 5k,
BC should be such that,
AC - AB < BC < AC + AB
12k - 5k < BC < 12k + 5k
7k < BC < 17 k
However, BC = 10.9k. Clearly, such a triangle is possible and hence, such value of sec A is possible Hence, the given statement is true
(iii)Abbreviation used for cosecant of angle A is cosec A. And Cos A is the abbreviation used for cosine of angle A Hence, the given statement is false
(iv)Cot A is not the product of cot and A. It is the cotangent of ∠A
Hence, the given statement is false
(v) 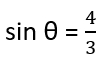
In a right-angled triangle, hypotenuse is always greater than the remaining two sides. Therefore, such value of sin θ is not possible
Hence, the given statement is false
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply