Solve the following pairs of equations by reducing them to a pair of linear equations:

(i)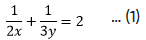

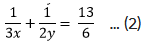
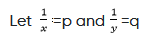
then the equations becomes.

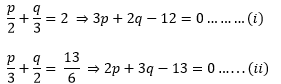
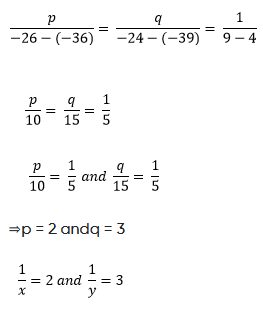
(ii) 2/√x +3/√y = 2
4/√x - 9/√y = -1

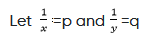
Putting this in (1) and (2), we get

2p + 3q = 2 … (i)

4p − 9q = −1 … (ii)

Multiplying (i) by 3, we get

6p + 9q =6 … (iii)

Adding equation (ii) and (iii),we obtain

10p =5

p = 1/2

Putting value of p in (i), we get

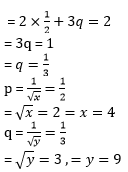
Hence,x = 4 and y = 9.

(iii) 4/x + 3y = 14
3/x - 4y = 23

let p = 1 / x

Putting value of p in equation, we get

4p + 3y = 14 … (i)

3p − 4y = 23 … (ii)

By cross-multiplication,we get,

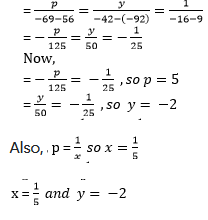
(iv)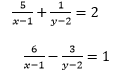

putting 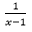= p and 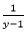=q,we get,

=5p+q =2 … (i)
=6p-3q =1 … (ii)

Now, multiplying equation (i) by 3,we get

15p +3q = 6 … (iii)

Adding equation (ii) and (iii)

21 p = 7

p = 7/21

p = 1 / 3

putting value of p in equation (iii),we get,

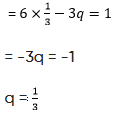
we know that,

=y - 2 = 3
y = 5

Hence,x=4 and y =5

(v) 7x − 2y = 5xy … (1)

8x + 7y = 15xy … (2)

Dividing both the equations by xy, we get

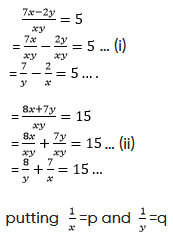
we get,

7q − 2p = 5 … (iii)

8q + 7p = 15 … (iv)

multiplying equation (iii) by 7 and equation (iv) by 2,we get,

49q - 14p =5 … (v)

16q + 14p = 30 … (vi)

After adding equation (v) and (vi),we get,
65q = 65
=q = 1

putting value of q in equation (iv), we get,

8 + 7p = 15
= 7p = 15 -8 = 7
= p =1

Now,

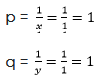
Hence,x = 1 and y = 1

(vi) 6x + 3y − 6xy = 0 … (1)

2x + 4y − 5xy = 0 … (2)

Dividing both the equations by xy, we get

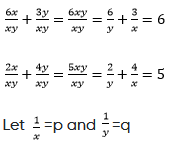
Putting these in (3) and (4), we get

6q + 3p – 6 = 0 … (5)

2q + 4p – 5 = 0 … (6)

From (5),

3p = 6 − 6q

⇒p = 2 − 2q

Putting this in (6), we get

2q + 4 (2 − 2q) – 5 = 0

⇒ 2q + 8 − 8q – 5 = 0

⇒ −6q = −3⇒q = ½

Putting value of q in (p = 2 – 2q), we get

p = 2 – 2 (½) = 2 – 1 = 1

Putting values of p and q in (1/x = p and 1/y = q), we getx = 1 andy = 2

Putting this in (1) and (2), we get

10p + 2q = 4 … (3)

15p − 5q = −2 … (4)

From equation (3),

2q = 4 − 10p

⇒q = 2 − 5p … (5)

Putting this in (4), we get

15p – 5 (2 − 5p) = −2

⇒ 15p – 10 + 25p = −2

⇒ 40p = 8⇒p = 1/5

Putting value of p in (5), we get

q = 2 – 5 (1/5) = 2 – 1 = 1

Putting values of p and q in (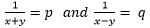), we get

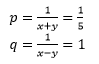
⇒x +y = 5 … (6) andx –y = 1 … (7)

Adding (6) and (7), we get

2x = 6 ⇒x = 3

Puttingx = 3 in (7), we get

3 –y = 1

⇒y = 3 – 1 = 2

Therefore,x = 3 andy = 2

(viii) 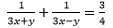… (1)

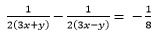… (2)

Let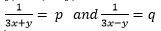

Putting this in (1) and (2), we get

p +q = 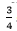and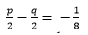

⇒ 4p + 4q = 3 … (3) and 4p − 4q = −1 … (4)

Adding (3) and (4), we get

8p = 2 ⇒p = ¼

Putting value of p in (3), we get

4 (¼) + 4q = 3

⇒ 1 + 4q = 3

⇒ 4q = 3 – 1 = 2

⇒q = ½

Putting value of p and q,we get,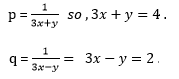

 

⇒ 3x +y = 4 … (5) and 3x –y = 2 … (6)

Adding (5) and (6), we get

6x = 6 ⇒x = 1

Puttingx = 1 in (5) , we get

3 (1) +y = 4

⇒y = 4 – 3 = 1

Therefore,x = 1 andy = 1