Represent √9.23 on the number line.

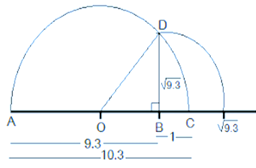
Step 1: Draw a line segment of 9.3 unit. Then, extend it to C so that BC = 1 unit.

Step 2: Now, AC = 10.3 units. Find the center of AC and mark it as O

Step 3: Draw a semi-circle with radius OC and center O

Step 4: Draw a perpendicular line BD to AC at point B intersecting the semi-circle at D. And then, join OD

Step 5: Now, OBD is a right angled triangle

Here, OD = 10.3/2 (Radius of semi-circle)

OC = 10.3/2

BC = 1

OB = OC – BC

= (10.3/2 - 1)

= 8.3/2

Using Pythagoras theorem,

OD² = BD² + OB²

(10.3/2)² =  BD²  + (8.3/2)²

BD²  = (10.3/2)² - (8.3/2)²

BD²  = (10.3/2 - 8.3/2) (10.3/2 + 8.3/2)

BD²  = 9.3

BD = √9.3

Thus, the length of BD is √9.3

Step 6: Taking BD as radius and B as the center, construct an arc which touches the line segment.

Now, the point where it touches the line segment is at a distance of √9.3 from O as shown in the figure below