Share
(i)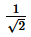
(ii)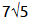
(iii)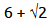
Question
(i) Let is rational.
Therefore, we can find two integers p & q where, q ≠0 such that
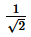 is rational as p and q are integers.
is rational as p and q are integers.
Therefore, is rational which contradicts to the fact that is irrational.
Hence, our assumption is false and is irrational.
(ii)Let is rational.
Therefore, we can find two integers p & q where, q≠0 such that
for some integers p and q
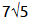 is rational as p and q are integers.
is rational as p and q are integers.
Therefore, should be rational.
This contradicts the fact that is irrational.
Therefore our assumption that is rational is false.
Hence, is irrational.
(iii)Let be rational.
Therefore, we can find two integers p & q where q≠0, such that
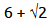
Since p and q are integers, is also rational
Hence, should be rational, this contradicts the fact that is irrational.
So, our assumption is false and hence, is irrational.
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply