Share
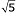 is irrational.
is irrational.
Question
Let is a rational number.
we can find two co-prime numbers p, q (q ≠ 0) such that
Let ‘p’ and ‘q’ have a common factor other than 1.
Therefore, p2 is divisible by 5 and it can be said that ‘p’ is divisible by 5.
Let p = 5k, where k is an integer
(5k)2 = 5q2 this mean that q2 is divisible by 5 and hence, q is divisible by 5.
q2 = 5k2 this implies that p and q have 5 as a common factor.
And this is a contradiction to the fact that p and q are co-prime.
Hence, cannot be expressed as or it can be said that is irrational.
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply