Prove that , the normal to y square equal to 12 x

Sol. So here the parabola is y²=12x

If we compare with y²=4ax then we get, a=3

Then, parametric form of a point on the parabola is (at²,2at)

Here (3,6) is on parabola.

so, 2at = 6 t = 6/2a = 6/2 x3 = 6/6 = 1

then the equation of normal,

y+tx=2at+at³

y+x=6+3 y=9-x

If we put this value of y in parabola

(9-x)²=12x

81-18x+x²=12x

x²-18x+81-12x=0

x²-30x+81=0

x²-27x-3x+81=0

x(x-27)-3(x-27)=0

(x-27)(x-3)=0 x=3,27

We know already (3,6) is on the normal.

So, x = 27 Then, y = 9-x = 9 - 27 = -18

Then (27,-18) is also another intersection point with parabola.

Circle with normal chord as diameter

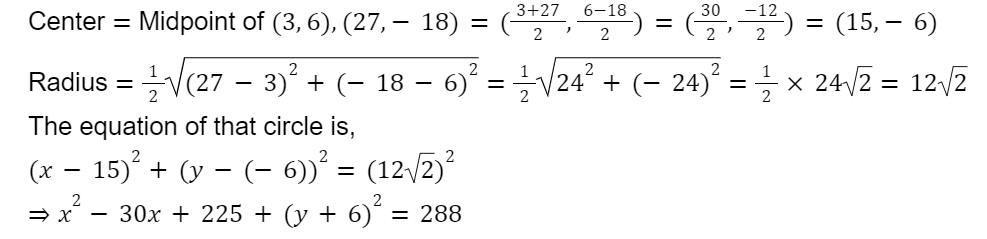
x²-30x+225+y²+12y+36-288=0

x²+y²-30x+12y-27=0, proved

Final Answer:

Hence it is proved that, Prove that , the normal to y2=12x at (3,6) meets the parabola again in (27,-18) & circle on this normal chord as diameter is x²+y²-30x+12y-27=0.