Share
.png)
Question
(i) Number of terms can be calculated as follows:
an = a + (n – 1)d
Or, 50 = 5 + (n – 1)3
Or, (n – 1)3 = 50 – 5 = 45
Or, n – 1 = 15
Or, n = 16
Sum of n terms can be given as follows:
.png)
(ii) Common difference can be calculated as follows:
an = a + (n – 1)d
Or, 35 = 7 + 12d
Or, 12d = 35 – 7 = 28
Or, d = 7/3
Sum of n terms can be given as follows:
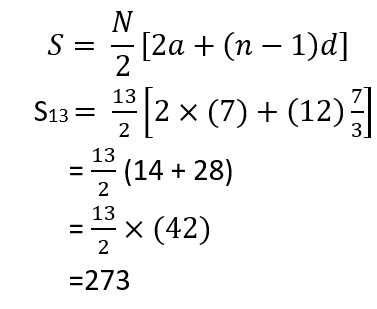
(iii) First term can be calculated as follows:
an = a + (n – 1)d
Or, 37 = a + 11 x 3
Or, a = 37 – 33 = 4
Sum of n terms can be given as follows:
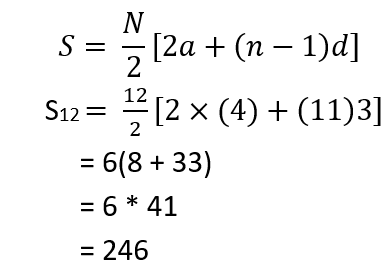
(iv) Sum of n terms can be given as follows:
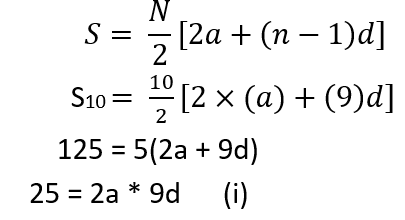
According to the question; the 3rd term is 15, which means;
a + 2d = 15 (ii)
Now,
Subtracting equation (ii) from equation (i), we get;
2a + 9d – a – 2d = 25 – 15
Or, a + 7d = 10 (iii)
Subtracting (ii) from equation (iii), we get;
a + 7d – a – 2d = 10 – 15
Or, 5d = - 5
Or, d = - 1
Now,
Substituting the value of d in equation (2), we get;
a + 2(- 1) = 15
Or, a – 2 = 15
Or, a = 17
10th term can be calculated as follows;
a10 = a + 9d
= 17 – 9 = 8
Thus, d = - 1 and 10th term = 8
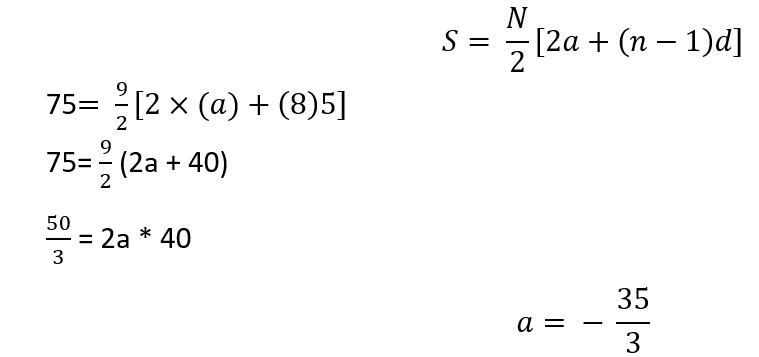 Now,
Now,
9th term can be calculated as follows:
a9 = a + 8d
=35/3+40
=85/3
(vi) Sum of n terms can be given as follows:
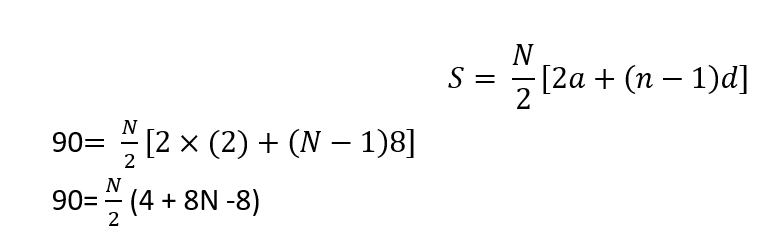
90 = N(2 +4N -4)
4N2 -2N -90 =0
2N2 -N -45 =0
(2N +9)(N -5)
Hence, n = - 9/2 and n = 5
Rejecting the negative value,
We have n = 5
Now, 5thterm will be:
a5 = a + 4d
= 2 + 4 x 8
= 2 + 32 = 34
(vii) Sum of n terms can be given as follows:
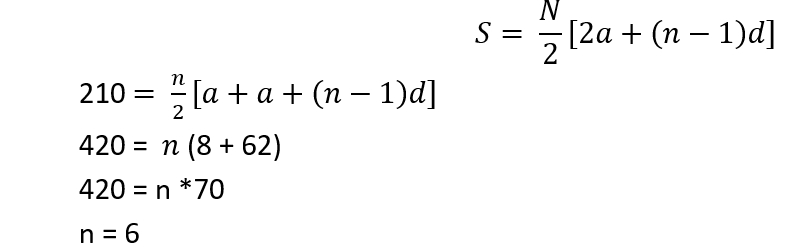
Now, for calculating d:
a6 = a + 5d
Or, 62 = 8 + 5d
Or, 5d = 62 – 8 = 54
Or, d = 54/5
viii. Sum of n terms can be given as follows:
.png)
We know;
an = a + (n – 1)d
Or, 4 = a + (n – 1)2
Or, 4 = a + 2n – 2
Or, a + 2n = 6
Or, 2n = 6 – a
Or, n = (6 – a)/2 (ii)
Using (i) and (ii):
-28/a+4=6-a/2
-56 = (6 –a)(a +4)
24 + 2a – a2 = -56
a2 -2a -80= 0
(a + 8)(a – 10)= 0
Therefore, a = - 8 and a = 10
As a is smaller than 10 and d has positive value, hence we’ll take a = - 8
Now, we can find the number of terms as follows:
an = a + (n – 1)d
4 = - 8 + (n – 1)2
(n – 1)2 = 4 + 8 = 12
n – 1 = 6Or, n = 7
Hence, n = 7 and a = -
(ix) Sum of n terms can be given as follows:
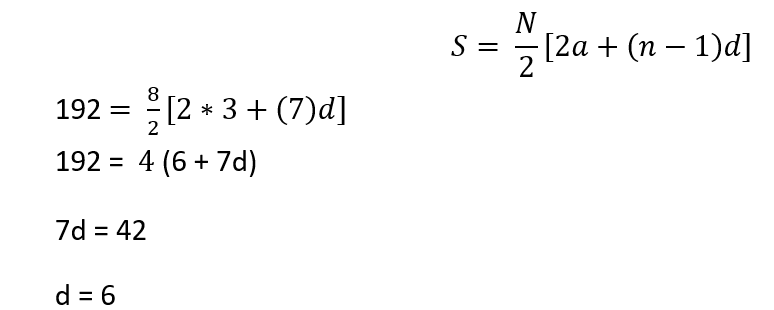
(x) Sum of n terms can be given as follows:
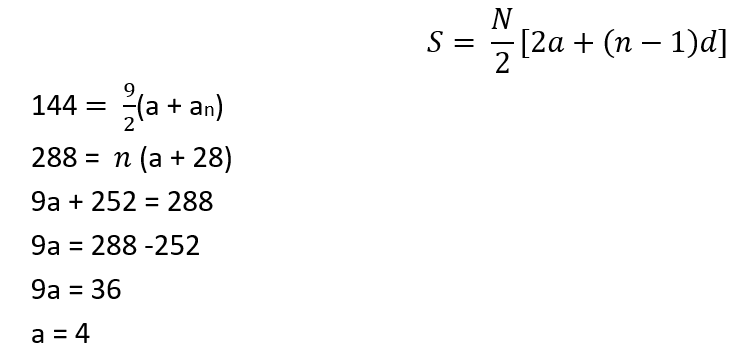
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply