Share
(i)2x2 – 3x + 5 = 0
- If b2 − 4ac > 0 → two distinct real roots>/li>
- If b2 − 4ac = 0 → two equal real roots
- If b2 − 4ac < 0 → no real roots
(ii) 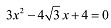
(iii) 2x2 – 6x + 3 = 0
Question
(i) 2x2 – 3x + 5 = 0
Comparing this equation with ax2 + bx + c = 0, we obtain,
a = 2, b = −3, c = 5
Discriminant = b2 − 4ac = (− 3)2 − 4 (2) (5) = 9 − 40 = −31
As, b2 − 4ac < 0,
Therefore, no real root is possible for the given equation.
(ii) 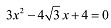
Comparing this equation with ax2 + bx + c = 0,
we obtain,
a = 3
b = -4√3
c = 4
=Discriminant = 48 − 48 = 0
As, b2 − 4ac = 0,
Therefore, real roots exist for the given equation and they are equal to each other.
And the roots will be and .
Therefore, the roots are and .
(iii) 2x2 – 6x + 3 = 0
Comparing this equation with ax2+bx + c = 0,
we obtain,
a = 2, b = −6, c = 3
Discriminant = b2 − 4ac = (− 6)2 − 4 (2) (3) = 36 − 24 = 12
As, b2 − 4ac > 0,
Therefore, distinct real roots exist for this equation as follows.
So, the roots are or .
solved
5
wordpress
4 mins ago
5 Answer
70 views
+22

Leave a reply