A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumference

Explanation:

The disc can be written as

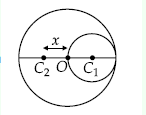
The mass of the dics can be calculated M=π〖(2R)〗^2 σ where σ is the mass per unit area.

The mass of removed disc  M₁=π(R)² σ

⇒M₁ = 1/4 M

The mass of the remaining disc

M₂=M-M₁

=M-1/4 M

=3/4 M

And now we can write

M₁×OC₁=M₂×OC₂

⇒M/4 R=3M/R x

⇒x=R/3=σR

⇒σ=1/3