Derivatives Of A Function In Parametric Form

Parametric equations are a powerful mathematical tool that can be used to solve complex problems. They allow you to express a set of equations in terms of a single variable, called the parameter. In this article, we'll explore the derivatives of functions in parametric form, their applications, and provide some solved examples.

Introduction to Parametric Equations

Parametric equations are a way to represent a set of variables as functions of a single parameter. This parameter is used to express the values of the variables in a continuous manner, and it changes continuously over time. The derivatives of functions in parametric form are crucial because they help us understand the rate of change of the variables, which is essential in many real-world applications.

What is a parametric equation?

A parametric equation is a mathematical representation of a set of variables that are expressed as functions of a parameter. The parameter can be any real number, and it is used to calculate the values of the variables continuously. In a parametric equation, the variables are functions of the parameter, and the value of the variables changes as the parameter changes. For example, a simple parametric equation can be represented as x=t2 and y=2t, where are the x and y variables, and t is the parameter.

In other words, A parametric equation is a way of expressing a set of equations in terms of a single parameter. This parameter can be anything from time, distance, or velocity. It is a very powerful tool that is used for solving more complex equations.

For example, the equation for a circle is usually expressed in terms of x and y:

x2+y2=r2

This equation can also be expressed in terms of a single parameter, t, as follows:

x=rcos(t)

y=rsin(t)

This is known as a parametric equation, where t is the parameter. 

Parametric Differentiation

If y is specified as a function of x and x = f(t) are two differentiable functions of the parameter t, then:

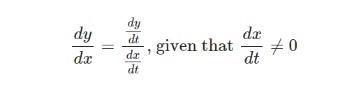
Or

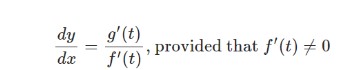
When the functions are represented in a parametric form, it is obvious that this is the first derivative of the function y with respect to x. Calculating the second derivative is as follows:

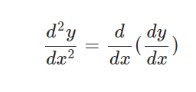
Relying on the First Order Parametric Differentiation once more, but this time using dydx as a function of the parameter t:

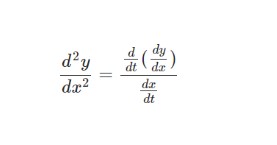
Higher order derivatives may also be calculated similarly. The essential thing to bear in mind is that the parameter t will always be a function of every derivative that is calculated. Additionally, it is clear because x and y are functions of t in reality. To close the deal, let's look at some examples that have been solved.

Applications of Parametric Equations

Parametric equations have a wide range of applications in various fields, including:

1. Physics: Parametric equations are used to describe the motion of objects, such as the trajectory of a projectile or the path of a planet orbiting the sun.
2. Engineering: Parametric equations are used in computer-aided design (CAD) software to create complex shapes and surfaces.
3. Economics: Parametric equations can be used to model economic relationships, such as supply and demand curves.
4. Mathematics: Parametric equations are used in calculus to study the properties of curves and surfaces, such as their tangent lines and curvature.

Conclusion

In conclusion, the derivatives of functions in the parametric form are a crucial tool in calculus and have various applications in real-life scenarios. They are used to study the rate of change of variables expressed as functions of a parameter, and they help in understanding the behaviour of systems that change continuously with time. The calculation of derivatives of functions in parametric form is straightforward, and it can be done using simple differentiation rules.